Les seules forces données, extérieures à
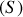 , sont la pesanteur, d'accélération
, sont la pesanteur, d'accélération
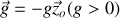 . La liaison en
. La liaison en
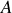 est sphérique et parfaite (liaison rotule). La liaison en
est sphérique et parfaite (liaison rotule). La liaison en
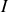 entre
entre
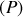 et
et
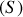 est ponctuelle, de résultante :
est ponctuelle, de résultante :
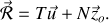
Question 1
Etablir, à partir du théorème du moment dynamique en
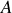 appliqué à
appliqué à
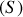 , trois équations différentielles du mouvement de
, trois équations différentielles du mouvement de
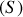 , ne comportant que les données, les angles d'Euler et leurs dérivées par rapport au temps et les composantes de
, ne comportant que les données, les angles d'Euler et leurs dérivées par rapport au temps et les composantes de
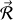 .
.
On suppose que le mouvement à lieu, dorénavant, sans glissement.
Question 2
Déduire de la relation de non-glissement en
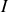 l'une relation entre
l'une relation entre
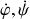 et
et
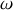 .
.
Question 3
Trouver alors l'expression de
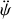 , de
, de
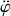 et de
et de
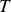 en fonction de
en fonction de
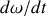 .
.
Question 4
Les conditions initiales (à
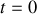 ) du mouvement sont telles que
) du mouvement sont telles que
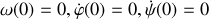 . Calculer
. Calculer
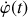 et
et
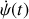 en fonction de
en fonction de
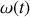 .
.
Question 5
Déterminer
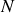 en fonction de
en fonction de
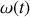 . On suppose que
. On suppose que
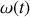 est une fonction croissante du temps pour
est une fonction croissante du temps pour
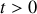 . Montrer qu'il existe une valeur
. Montrer qu'il existe une valeur
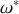 de
de
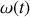 pour laquelle
pour laquelle
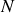 s'annule et calculer
s'annule et calculer
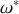 . Expliquer intuitivement ce qui se passe lorsque
. Expliquer intuitivement ce qui se passe lorsque
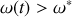 .
.




