Réponse 1
Par définition, les éléments de réduction du torseur cinétique de
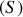 dans le référentiel
dans le référentiel
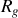 sont le moment cinétique de
sont le moment cinétique de
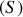 en un point
en un point
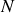 ,
,
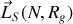 et la résultante cinétique de
et la résultante cinétique de
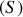
 , où
, où
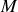 est la masse de
est la masse de
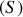 et
et
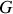 son barycentre. Par rapport au point
son barycentre. Par rapport au point
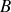 , le moment cinétique s'exprime, grâce au théorème de Koenig, sous la forme :
, le moment cinétique s'exprime, grâce au théorème de Koenig, sous la forme :
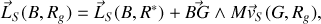
où
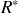 est le référentiel barycentrique lié au solide
est le référentiel barycentrique lié au solide
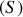 . Or, la barre
. Or, la barre
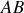 est supposée sans masse.
est supposée sans masse.
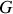 est donc confondu avec le point
est donc confondu avec le point
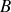 , barycentre du disque
, barycentre du disque
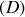 ,
,
 et les grandeurs cinétiques ne se rattachent plus qu'au disque
et les grandeurs cinétiques ne se rattachent plus qu'au disque
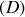 .
.
Dans
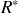 , de repère associé
, de repère associé
 , le mouvement est composé d'une rotation autour de l'axe
, le mouvement est composé d'une rotation autour de l'axe
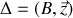 à la vitesse angulaire
à la vitesse angulaire
 et d'une rotation autour de l'axe
et d'une rotation autour de l'axe
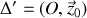 à la vitesse angulaire
à la vitesse angulaire
 . Les deux axes
. Les deux axes
 et
et
 étant fixes, on a la relation :
étant fixes, on a la relation :

où
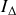 et
et
 sont les moments d'inertie du solide
sont les moments d'inertie du solide
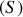 respectivement par rapport aux axes
respectivement par rapport aux axes
 et
et
 .
.
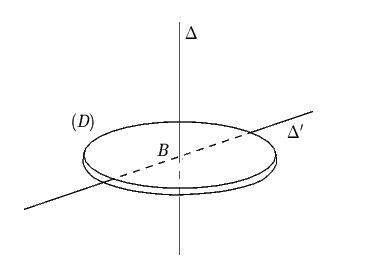
L'axe
 passant par le centre
passant par le centre
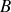 du disque
du disque
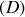 étant perpendiculaire à
étant perpendiculaire à
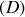 , on a
, on a
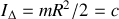 .
.
Pour le calcul de
 , on peut utiliser la relation
, on peut utiliser la relation
 (à démontrer, par exemple en s'inspirant de la question 1.a) du problème I). Cette relation est valable en négligeant l'épaisseur du disque
(à démontrer, par exemple en s'inspirant de la question 1.a) du problème I). Cette relation est valable en négligeant l'épaisseur du disque
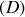 devant son rayon, et conduit à
devant son rayon, et conduit à
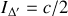 .
.
En regroupant les différents termes, il vient :

La résultante cinétique se calcule quant à elle en utilisant la relation cinématique entre le point
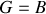 et le point
et le point
 du solide
du solide
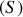 :
:
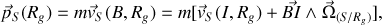
ce qui donne :

Les éléments de réduction du torseur cinétique de
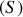 au point
au point
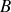 sont donc :
sont donc :

Remarque :
si l'on n'utilise pas le théorème de Koenig, un calcul direct donne

puisque la barre AB est sans masse.
Par ailleurs
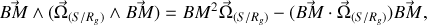
D'où

Réponse 2
Les éléments de réduction du torseur cinétique au point
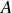 sont par définition :
sont par définition :
On arrive, en utilisant le résultat de la question précédente, à l'expression des éléments de réduction du torseur cinétique au point
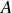 :
:
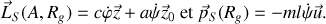
Réponse 3
Par définition, les éléments de réduction au point
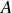 du torseur dynamique de
du torseur dynamique de
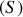 sont le moment dynamique de
sont le moment dynamique de
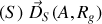 et la résultante dynamique de
et la résultante dynamique de
 où
où
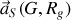 est l'accélération au point
est l'accélération au point
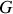 du solide
du solide
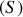 dans
dans
 .
.
Le point A étant fixe dans le référentiel galiléen, on a :

Avec cette dernière relation, on déduit les éléments de réduction du torseur dynamique au point
 :
:
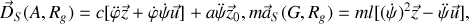
car les vecteurs
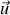 et
et
 sont des vecteurs tournants autour de l'axe
sont des vecteurs tournants autour de l'axe
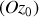 , ce qui impose les relations
, ce qui impose les relations







