Réponse 1
L'application du théorème du moment dynamique au point
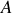 , au solide
, au solide
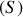 dans le référentiel galiléen donne :
dans le référentiel galiléen donne :

où
-
 est le moment en
est le moment en
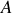 du poids
du poids
-
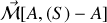 est le moment en
est le moment en
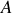 des efforts de contact de la liaison au point
des efforts de contact de la liaison au point
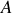
-
 est le moment en
est le moment en
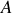 des efforts de contact en
des efforts de contact en
 entre la plaque
entre la plaque
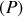 et le solide
et le solide
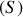 .
.
La liaison en
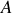 est supposée parfaite : il y a possibilité de pivotement en
est supposée parfaite : il y a possibilité de pivotement en
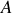 sans frottements de pivotement et de roulement en
sans frottements de pivotement et de roulement en
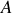 sans frottements de roulement, ce qui implique
sans frottements de roulement, ce qui implique
 .
.
De même, au point de contact
 entre
entre
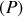 et
et
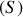 , la liaison est supposée ponctuelle : le roulement s'effectue sans frottements de roulement. On en déduit
, la liaison est supposée ponctuelle : le roulement s'effectue sans frottements de roulement. On en déduit
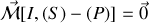 .
.
D'où :
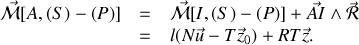
De même, la tige
 étant sans masse,
étant sans masse,
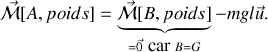
On obtient ainsi les trois équations différentielles du mouvement de
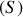 :
:

Réponse 2
L'hypothèse de mouvement sans glissement conduit à
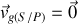 . D'après la question 1.3., on a alors la relation :
. D'après la question 1.3., on a alors la relation :

Réponse 3
La combinaison des équations (2) et (3) de la question 3.1. fournit une relation entre
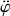 et
et
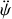 :
:
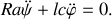
La combinaison des équations (4) et (5) permet d'aboutir aux relations demandées :
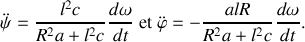
L'expression de
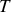 en fonction de
en fonction de
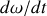 s'obtient alors à partir de l'équation (3) par exemple :
s'obtient alors à partir de l'équation (3) par exemple :
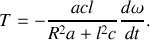
Réponse 4
A l'instant initial
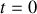 , toutes les vitesses angulaires sont nulles. La vitesse angulaire étant une fonction continue en
, toutes les vitesses angulaires sont nulles. La vitesse angulaire étant une fonction continue en
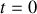 (sinon, cela conduirait à des accélérations et donc à des forces "infinies", ce qui n'est pas acceptable d'un point de vue physique), l'intégration des relations précédentes conduit à :
(sinon, cela conduirait à des accélérations et donc à des forces "infinies", ce qui n'est pas acceptable d'un point de vue physique), l'intégration des relations précédentes conduit à :

Réponse 5
D'après l'équation (1), on peut déterminer l'expression de
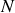 en fonction de
en fonction de
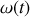 :
:
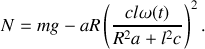
Puisque
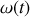 est une fonction croissante de
est une fonction croissante de
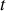 , positive pour tout
, positive pour tout
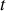 , il existe
, il existe
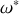 tel que
tel que
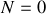 pour
pour
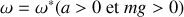 . L'expression précédente de
. L'expression précédente de
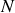 donne alors l'expression de
donne alors l'expression de
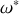 :
:
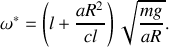
Pour
 , la composante verticale de la réaction du support
, la composante verticale de la réaction du support
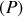 sur le solide
sur le solide
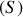 s'annule et change de signe. Ainsi, pour
s'annule et change de signe. Ainsi, pour
 , le solide
, le solide
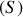 va décoller du plateau, tout en continuant à tourner sur lui-même et autour de l'axe
va décoller du plateau, tout en continuant à tourner sur lui-même et autour de l'axe
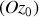 , puisque
, puisque
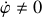 et
et
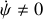 pour tout
pour tout
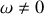 . Le solide
. Le solide
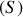 va donc, pour
va donc, pour
 , se comporter comme une toupie : il va tourner sur lui-même et avoir un mouvement de précession autour de l'axe de
, se comporter comme une toupie : il va tourner sur lui-même et avoir un mouvement de précession autour de l'axe de
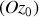 .
.




