Dans ce cas, les forces volumiques extérieures se réduisent à
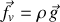
En se plaçant en régime permanent et en supposant constante, l'intégration de l'équation d'Euler suivant une ligne de courant
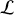 conduit à :
conduit à :
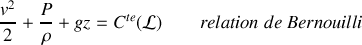
Cette constante est caractéristique de la ligne de courant considérée, et varie d'une ligne à l'autre. Si l'on suppose en outre l'écoulement irrotationnel (
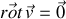 ) :
) :
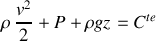
où la constante est cette fois la même pour tous les points du fluide.
La relation de Bernouilli est formellement identique au premier principe de la thermodynamique : elle traduit la conservation de l'énergie mécanique des particules fluides le long d'une ligne de courant (un élément de fluide de volume
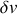 a une masse
a une masse
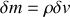 , et donc une énergie cinétique
, et donc une énergie cinétique
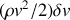 et une énergie potentielle de pesanteur
et une énergie potentielle de pesanteur
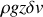 ; ainsi,
; ainsi,
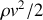 est la densité volumique d'énergie cinétique et
est la densité volumique d'énergie cinétique et
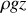 est la densité volumique d'énergie potentielle de pesanteur).
est la densité volumique d'énergie potentielle de pesanteur).
Pour une généralisation à des régimes dépendant du temps, on pourra consulter le problème II (partie I).
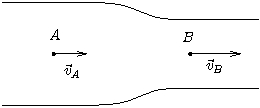
Exemple : L'effet Venturi
Considérons le tube de Venturi représenté sur la figure 1. L'aire de la section droite est
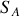 en
en
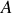 et
et
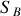 en
en
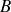 (
(
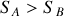 ). En régime permanent, la conservation du débit impose
). En régime permanent, la conservation du débit impose
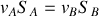 , d'où
, d'où
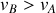 .
.
Par ailleurs, la relation de Bernouilli s'écrit, pour
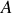 et
et
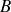 de même altitude appartenant à une même ligne de courant :
de même altitude appartenant à une même ligne de courant :
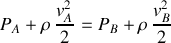
On en déduit
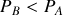 : les régions de grande vitesse sont les régions de basse pression, et réciproquement. Ce phénomène est appelé effet Venturi.
: les régions de grande vitesse sont les régions de basse pression, et réciproquement. Ce phénomène est appelé effet Venturi.




