Le théorème d'OSTROGRADSKY (flux-divergence) permet d'obtenir, à partir de la deuxième des équations locales, le théorème de GAUSS :
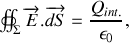
où
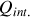 représente la charge totale intérieure à la surface fermée
représente la charge totale intérieure à la surface fermée
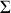 considérée. Lorsque l'on fait circuler le champ électrique le long d'un chemin allant d'un point 1 à un point 2, la première des équations locales fournit la relation
considérée. Lorsque l'on fait circuler le champ électrique le long d'un chemin allant d'un point 1 à un point 2, la première des équations locales fournit la relation

Exemple :
Dans de nombreux cas, le théorème de Gauss, adjoint à des considérations de symétrie, permet de trouver le champ engendré par une distribution de charges. On réserve en général le calcul direct, par les formules que nous allons énoncer dans le prochain paragraphe, à de rares cas. Calculons par exemple le champ d'une distribution de charges se présentant sous la forme d'une coquille sphérique infiniment mince, de centre
 et de rayon
et de rayon
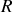 et portant une charge surfacique uniforme
et portant une charge surfacique uniforme
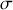 . La symétrie sphérique du problème restreint le nombre des variables pertinentes à la seule coordonnée radiale
. La symétrie sphérique du problème restreint le nombre des variables pertinentes à la seule coordonnée radiale
 . De plus, en un point
. De plus, en un point
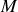 quelconque de l'espace, tous les plans contenant
quelconque de l'espace, tous les plans contenant
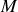 et divisant la coquille en deux moitiés sont plans de symétrie de la distribution ; le champ
et divisant la coquille en deux moitiés sont plans de symétrie de la distribution ; le champ
 est donc contenu dans chacun d'eux :
est donc contenu dans chacun d'eux :
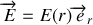 (
(
 est le vecteur unitaire radial des coordonnées sphériques). Appliquons le théorème de GAUSS en choisissant comme surface d'intégration la sphère
est le vecteur unitaire radial des coordonnées sphériques). Appliquons le théorème de GAUSS en choisissant comme surface d'intégration la sphère
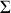 de rayon
de rayon
 . Il vient
. Il vient
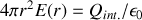 . On distingue alors deux régions. Dans la première (l'intérieur de la coquille qui est vide de charges) le champ est nul :
. On distingue alors deux régions. Dans la première (l'intérieur de la coquille qui est vide de charges) le champ est nul :
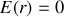 pour
pour
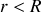 . A l'extérieur en revanche le champ s'écrit
. A l'extérieur en revanche le champ s'écrit
 c'est-à-dire que tout se passe pour
c'est-à-dire que tout se passe pour
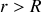 comme si l'on avait une charge ponctuelle
comme si l'on avait une charge ponctuelle
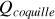 placée en
placée en
 . Notons qu'en écrivant que
. Notons qu'en écrivant que
 , on retrouve que le champ subit au passage de la surface chargée, à laquelle il est perpendiculaire, une discontinuité
, on retrouve que le champ subit au passage de la surface chargée, à laquelle il est perpendiculaire, une discontinuité
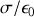 .
.




