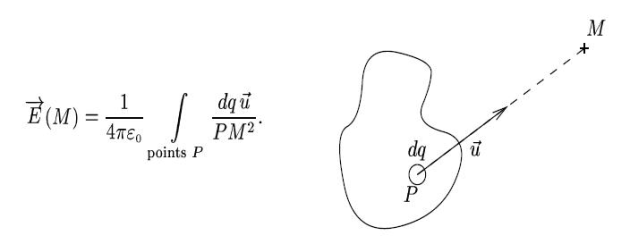
Soit
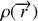la densité volumique de charge. Un volume élémentaire
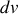contient la charge élémentaire
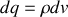. L'expression du champ régnant en un point
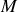est (
est 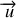le vecteur unitaire joignant
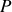à
:
)
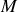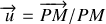Figure 2 : Notations employées. Dans l'approximation dipolaire,
.
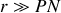Dans le cas où le domaine chargé ne s'étend pas jusqu'à l'infini, l'expression du potentiel est quant à elle
.
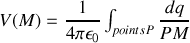On vérifie que les expressions précédentes permettent de retrouver les formules usuelles dans le cas de charges ponctuelles.
Remarque :
La linéarité des équations reliant le champ électrostatique à la densité de charge est à l'origine du principe dit de superposition : le champ créé par deux domaines de charges est la somme des champs créés par chacun d'eux.
