Les équations de la magnétostatique sont
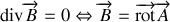
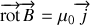
Si l'on combine ces deux relations, on obtient pour le potentiel vecteur
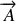une équation analogue à celle de POISSON-LAPLACE pour le potentiel électrostatique :
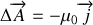
On a posé pour cela que
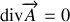ce qui est mathématiquement possible et usuellement utilisé (on qualifie ce choix de ”condition de jauge”).
Les conditions de raccordement à la traversée d'une surface parcourue par des courants de densité surfacique
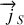sont quant à elles
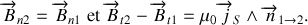
Remarque :
La composante du champ normale à la surface est donc continue à la traversée de la surface. La composante transverse est en revanche discontinue.
