La première des deux équations locales vérifiées par le champ magnétique indique que celui-ci est à flux conservatif, c'est-à-dire que pour toute surface fermée
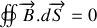
La circulation de
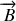le long d'un contour fermé
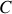donne quant à elle, en utilisant la deuxième des équations locales, le théorème d'AMPERE
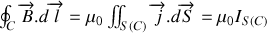
où
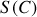est une surface s'appuyant sur le contour
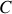. Les courants qui ”percent” cette surface dans le sens positif défini par l'orientation de
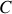(en utilisant la ”règle du tire-bouchon”), sont comptabilisés avec un signe positif.
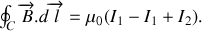
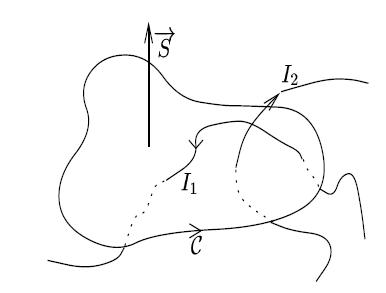
Exemple :
le théorème d'AMPERE est fréquemment utilisé pour calculer le champ magnétique créé par une distribution de courant. Considérons un fil vertical rectiligne infini, parcouru par un courant
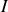dans le sens ascendant. Adoptons le système des coordonnées cylindriques, la verticale ascendante définissant l'axe
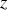. La distribution de courant est invariante par rotation autour de l'axe
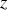, et par translation suivant cet axe. Par conséquent, la seule variable pertinente du problème est la coordonnée radiale
:
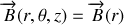. Considérons en outre un point
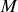quelconque de l'espace (en dehors du fil). Le plan passant par
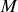et contenant le fil est un plan de symétrie de la distribution de courant ; le champ magnétique en
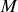lui est donc perpendiculaire et ainsi
.
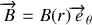Pour appliquer le théorème d'AMPERE, choisisons pour contour
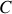un anneau de rayon
et d'axe le fil. Ce cercle est orienté par l'axe
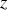et la règle du tire-bouchon. Il vient
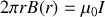ce qui nous permet de connaître le champ magnétique en tout point de l'espace, hors du fil :
.
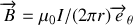