Réponse 1
Tout plan de symétrie pour les courants est un plan d'antisymétrie pour le champ magnétique et réciproquement. Formellement cette affirmation se traduit comme suit. Soit
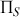un plan de symétrie et
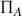un plan d'antisymétrie pour les courants. Cela signifie :
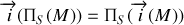
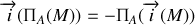
où
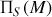et
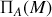représentent le symétrique du point
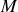par rapport au plan considéré et
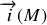est le vecteur densité de courant au point
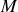. Les règles de symétrie s'écrivent :
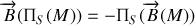
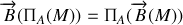
Complément :
On dit aussi que le champ magnétique est un pseudo-vecteur, c'est-à-dire que contrairement au champ électrique, il change de signe lorsque la convention d'orientation de l'espace change.
Remarque :
Le champ magnétique est contenu dans un plan d'antisymétrie des courants et il est orthogonal à tout plan de symétrie des courants. Bien entendu, on peut trouver des situations où ces plans n'existent pas.
Dans le cas qui nous intéresse, le plan
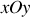est un plan de symétrie des courants, ce qui permet d'affirmer que
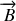est parallèle à l'axe des
.
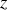Réponse 2
On ne s'intéresse qu'à la contribution suivant l'axe des
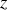de chaque dipôle élémentaire. Cette contribution provient à la fois de
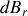et
:
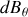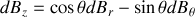
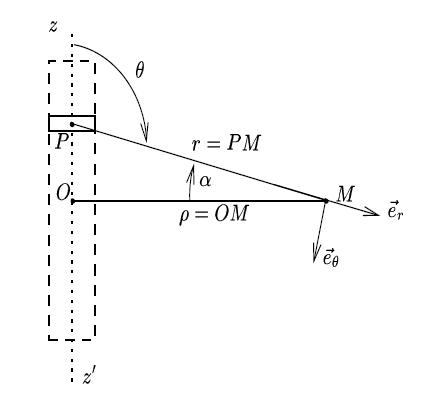
Nous avons montré à la question de la partie A que :
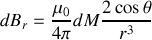
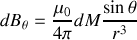
A l'aide de la figure 14, nous pouvons écrire
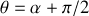et :
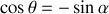
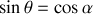
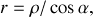
ce qui donne
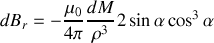
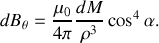
Ainsi,
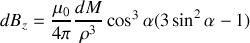
Réponse 3
On a
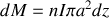avec
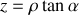, soit :
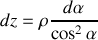
Nous pouvons maintenant écrire
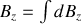sous la forme
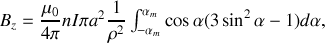
qui s'intègre en posant
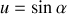pour donner :
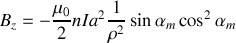
Réponse 4
a
Dans la limite où
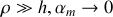puisque
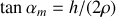. Plus précisément,
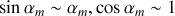et
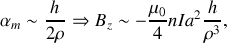
d'où
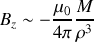
Compte tenu de
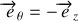pour
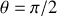, on retrouve bien le résultat de la question 1 :
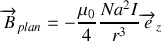
b
Dans la limite où
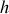devient très grand (sous-entendu, par rapport à
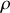), on a
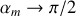par valeurs inférieures. Posons
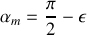avec bien sûr
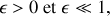
il vient :
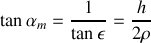
On a alors
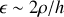, d'où
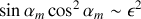
Ainsi,
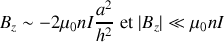
Ce résultat est indépendant de
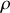mais il suppose
.
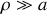Exemple :
A titre de vérification, lorsque
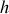tend vers l'infini, le champ magnétique tend vers
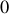. Dans ce cas, il est égal à
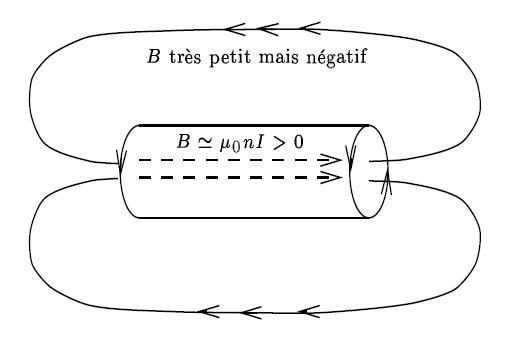
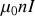à l'intérieur du solénoïde et nul en dehors. Le signe − présent dans l'expression précédente assure que les lignes de champ sont fermées (cf. figure 15 où le solénoïde est supposé très allongé :
)
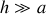