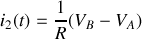Réponse 1
A des distances bien supérieures à
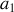, le champ magnétique est uniforme :
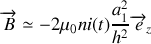
Par ailleurs, on peut vérifier que le potentiel vecteur correspondant à un champ magnétique constant est :
Dans la base
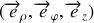des coordonnées cylindriques (à ne pas confondre avec la base
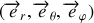des coordonnées sphériques), on a (voir figure 16)
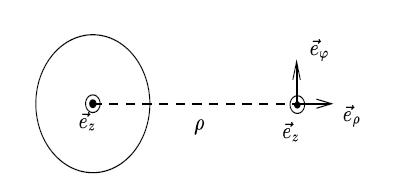
Ainsi,
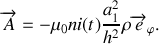
Le potentiel vecteur possède bien la même symétrie que les courants.
Réponse 2
En règle générale, le champ électromoteur a pour expression :
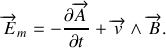
Ici, la spire est immobile et le champ
devient :
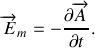
Nous supposerons les points
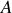et
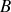très proches. La différence de potentiel induite aux bornes de la spire
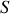est
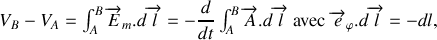
d'où
Réponse 3
Le circuit équivalent à la spire peut se schématiser comme sur la figure 17 qui précise la convention d'orientation pour l'intensité
.
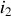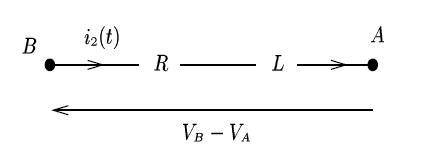
On a donc :
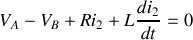
ce qui signifie que l'on observera un régime transitoire de temps caractéristique
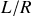avant qu'un régime sinusoïdal forcé ne s'établisse. Dans ce régime, la dépendance temporelle de
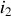est sinusoïdale. Pour résoudre l'équation différentielle précédente, il est commode de définir la grandeur complexe
:
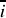où
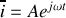et
.
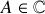Ainsi,
d'où
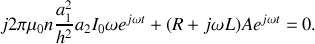
Nous en déduisons :
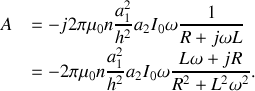
En définitive,
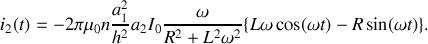
Comme il se doit, la partie inductive du signal (terme en
) est en quadrature, c'est-à-dire déphasée de
par rapport à la partie réactive
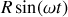. On peut vérifier que pour
, on a bien :
