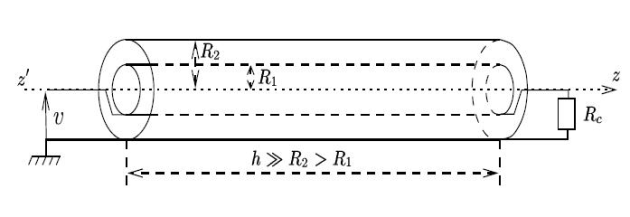
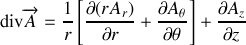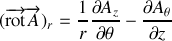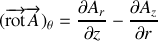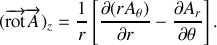Un signal sinusoïdal rapidement variable
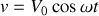 est appliqué à l'entrée du câble (figure 20). Si le câble est fermé à sa sortie sur une résistance
est appliqué à l'entrée du câble (figure 20). Si le câble est fermé à sa sortie sur une résistance
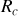 convenable, les ondes électromagnétiques sinusoïdales générées par le signal sont susceptibles de se propager uniquement dans le sens
convenable, les ondes électromagnétiques sinusoïdales générées par le signal sont susceptibles de se propager uniquement dans le sens
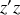 dans l'espace vide compris entre les conducteurs cylindriques. On se propose de déterminer
dans l'espace vide compris entre les conducteurs cylindriques. On se propose de déterminer
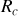 .
.
La fréquence angulaire
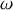 du signal est telle que les conducteurs peuvent être considérés comme parfaits ; la propagation de l'onde se fait sans perte.
du signal est telle que les conducteurs peuvent être considérés comme parfaits ; la propagation de l'onde se fait sans perte.
Question 1
Rappeler les équations de MAXWELL dans le vide.
Question 2
Parmi les différents modes possibles d'ondes susceptibles de se propager avec une fréquence donnée dans le câble, on envisage une onde à la fois transverse électrique et transverse magnétique. Les champs
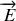 et
et
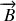 n'ont pas de composante
n'ont pas de composante
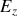 et
et
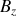 et leurs composantes radiale ou orthoradiale ne dépendent que de
et leurs composantes radiale ou orthoradiale ne dépendent que de
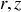 et
et
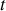 .
.
Compte-tenu des conditions aux limites à la surface des conducteurs parfaits, on cherche une onde qui s'écrit, en utilisant un système de coordonnées cylindriques et la notation complexe :
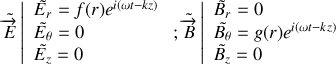
où
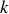 est une constante réelle positive. En se référant aux équations de MAXWELL :
est une constante réelle positive. En se référant aux équations de MAXWELL :
a
Exprimer
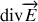 et montrer que
et montrer que
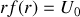 où
où
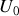 est une constante ;
est une constante ;
b
Utiliser l'équation de MAXWELL-FARADAY pour trouver une relation entre
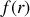 et
et
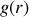 ;
;
c
En déduire à partir de l'équation de MAXWELL-AMPERE la relation qui lie
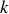 et
et
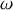 .
.
Question 3
On rappelle que l'expression générale du champ électrique
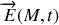 en fonction du potentiel scalaire
en fonction du potentiel scalaire
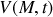 et du potentiel vecteur
et du potentiel vecteur
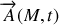 s'écrit :
s'écrit :
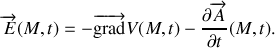
Compte-tenu de la symétrie du problème, on choisira ici
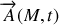 orienté suivant l'axe des
orienté suivant l'axe des
 . Calculer à l'instant
. Calculer à l'instant
 dans le plan
dans le plan
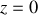 l'intégrale
l'intégrale
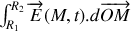 en utilisant pour
en utilisant pour
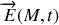 l'expression obtenue à la question précédente. En déduire
l'expression obtenue à la question précédente. En déduire
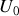 en fonction de
en fonction de
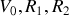 .
.
Question 4
a
Calculer la moyenne temporelle de la densité d'énergie électromagnétique
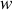 en un point
en un point
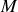 quelconque entre les deux conducteurs ainsi que la moyenne temporelle du vecteur de POYNTING
quelconque entre les deux conducteurs ainsi que la moyenne temporelle du vecteur de POYNTING
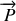 au même point. A quelle vitesse se propage l'énergie dans le câble ?
au même point. A quelle vitesse se propage l'énergie dans le câble ?
b
Calculer la valeur moyenne temporelle de la puissance totale transmise par la ligne coaxiale. Sachant que l'amplitude de la tension en sortie est
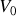 , en déduire la valeur qu'il convient de donner à la résistance
, en déduire la valeur qu'il convient de donner à la résistance
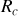 . Comparer la valeur obtenue pour
. Comparer la valeur obtenue pour
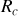 à
à
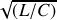 où
où
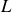 et
et
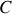 sont respectivement l'inductance propre et la capacité calculées précédemment.
sont respectivement l'inductance propre et la capacité calculées précédemment.
Application Numérique
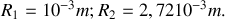
Calculer
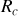 .
.
Formulaire :
On rappelle les expressions de
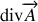 et
et
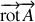 en coordonnées cylindriques :
en coordonnées cylindriques :