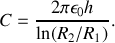Le câble coaxial étudié est tel que
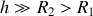, ce qui revient à négliger les effets de bords dans le calcul des champs : le câble pourra être considéré comme "infini" dans la direction
.
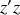Réponse 1
a
La distribution de charges est invariante par toute translation parallèlement à la direction
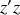, et par toute rotation autour de l'axe
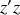. Le champ
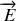ne dépend donc que de la coordonnée
:
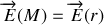
La distribution de charges est symétrique par rapport à tout plan
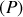contenant l'axe
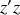. Le champ électrique est donc symétrique par rapport au plan
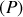. En particulier, pour tout point
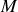appartenant à
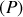, le champ
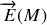est contenu dans ce plan
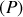. De même, la distribution de charges est symétrique par rapport à tout plan
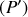perpendiculaire à l'axe
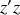. Le champ électrique est donc également symétrique par rapport à
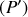. Pour un point
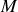appartenant à
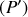, le champ électrique est contenu dans ce plan. En choisissant un point
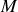appartenant à l'intersection des deux plans
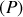et
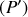, on en déduit que le champ électrique est radial. Ainsi :
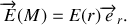
b
On applique le théorème de GAUSS
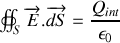
avec comme volume
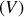un cylindre de longueur
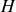arbitraire
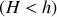et de rayon
, la normale à la surface
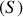étant orientée vers l'extérieur.
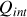est la charge totale comprise à l'intérieur du volume
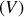. En utilisant la forme de
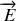donnée à la question précédente, on arrive à :
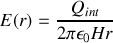
Il faut considérer trois régions d'espace :
1.
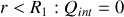
2.
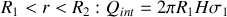
3.
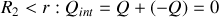car, pour
, on se trouve à l'extérieur du câble et les deux conducteurs sont en influence totale.
D'où :
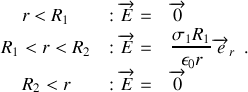
Remarque :
Le champ électrique est discontinu en
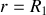et
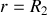et il vérifie bien les relations de passage.
Réponse 2
L'énergie électrostatique emmagasinée dans le câble peut s'écrire :
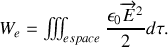
Comme le champ électrique est nul à l'extérieur du câble, l'énergie se réduit à :
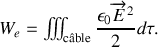
On utilise alors l'expression de
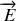calculée à la question précédente, les bornes d'intégration étant
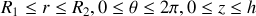. Le volume élémentaire
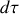s'exprime en coordonnées cylindriques par
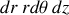. Il s'ensuit que
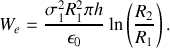
Or, du point de vue de l'électrostatique, le câble est un condensateur cylindrique de longueur
. On peut définir sa capacité
par la relation
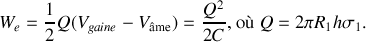
On en déduit l'expression de
:
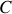