Réponse 1
Les équations de MAXWELL s'écrivent, dans le vide :
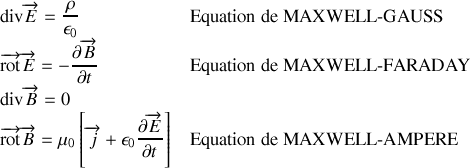
Réponse 2
On choisit un mode de propagation où les deux champs sont transverses. Pour les mêmes raisons qu'aux questions de la partie A et B, les modules des champs ne dépendent pas de la variable
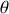. Les conducteurs étant supposés parfaits, les conditions aux limites sont :
la composante tangentielle du champ électrique est continue à la surface des conducteurs. Or, dans les conducteurs parfaits, on a
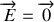. La composante tangentielle du champ électrique est donc nulle à la surface des conducteurs ;la composante normale du champ magnétique est nulle à la surface du conducteur, pour des raisons analogues.
Ceci explique la forme des champs
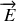et
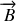proposée. Les ondes étudiées ne sont pas des ondes planes, il faudra donc utiliser les équations de MAXWELL de façon directe pour obtenir la relation de dispersion à l'intérieur du câble.
a
Avec l'expression de la divergence en coordonnées cylindriques fournie dans le formulaire, l'équation de MAXWELL-GAUSS dans l'espace entre les conducteurs (où
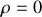), permet d'écrire :
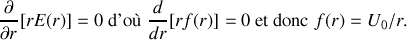
b
L'équation de MAXWELL-FARADAY conduit, en utilisant l'expression du rotationnel donnée dans le formulaire, à :
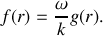
c
L'équation de MAXWELL-AMPERE, dans l'espace entre les conducteurs (où
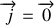), donne :
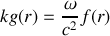
et
,
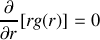ce qui conduit à la relation entre
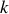et
:
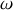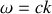. On obtient une expression analogue à la relation de dispersion dans le cas d'une onde plane dans le vide, bien que l'onde étudiée ne soit manifestement pas plane !
Une autre méthode pour obtenir la relation entre
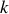et
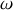serait de partir de l'équation d'onde
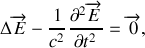
mais cela conduirait à des calculs nécessitant l'expression du laplacien en coordonnées cylindriques.
Réponse 3
Le système étant invariant par rotation autour de l'axe
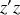, on a
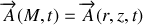. De plus, la distribution est antisymétrique par rapport à tout plan perpendiculaire à l'axe
:
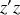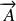possède la même propriété et peut se mettre sous la forme
.
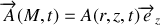On pose
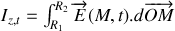. En remplaçant
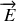par son expression déduite de la question de la partie C.2.
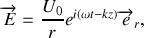
il vient :
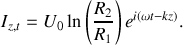
En particulier, à l'instant
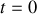dans le plan
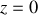, on a
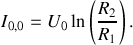
On peut réécrire
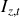grâce à l'expression de
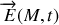proposée :
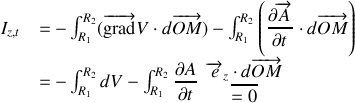
car, pour
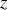et
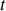fixés, on a
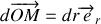. On a donc
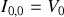à l'instant
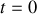dans le plan
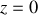. En comparant cette expression à celle obtenue précédemment, on peut écrire :
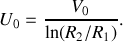
Réponse 4
a
Dans l'espace entre les conducteurs, le milieu est assimilé au vide, d'où :
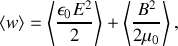
On peut calculer directement les valeurs moyennes temporelles (notées avec les crochets
) qui interviennent dans l'expression précédente, ou alors remarquer qu'avec la notation complexe :
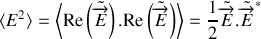
dans le cas d'une dépendance sinusoïdale en temps (c'est bien le cas ici). Il en va de même pour le champ magnétique. D'après la question 2, les champs
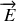et
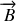s'écrivent, en notation complexe :
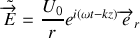
En substituant ces expressions dans la relation donnant
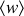, il vient :
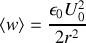
qui s'écrit encore, d'après la question précédente
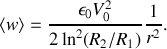
Dans le vide, le vecteur de POYNTING s'écrit en fonction des champs réels :
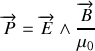
et sa valeur moyenne temporelle peut se mettre, en notation complexe, sous la forme :
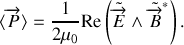
Finalement :
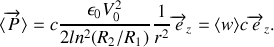
Le vecteur de POYNTING caractérise la propagation de l'énergie dans le câble. On constate donc que l'énergie électromagnétique se propage dans le câble à la vitesse
.
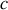b
La puissance transmise par la ligne est le flux du vecteur de POYNTING sur la section de la ligne située en
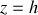, c'est-à-dire à la sortie du câble. D'après l'expression de
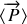calculée précédemment :
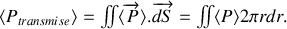
On en déduit :
.
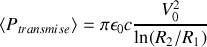Le câble étant fermé par une résistance
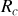et l'amplitude de la tension de sortie étant égale à
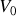, on a :
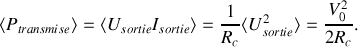
Ainsi :
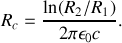
En utilisant les questions de la Partie A.2 et de la Partie B.2, on trouve :
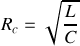
Application Numérique
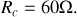
Complément :
La valeur de la résistance
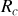calculée à la question 4.b) peut être déterminée en étudiant le câble coaxial d'un point de vue électrocinétique. En effet, le câble est modélisable par une capacité
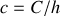par unité de longueur (on ne confondra pas
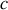avec la vitesse de la lumière !) et par une inductance propre
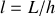par unité de longueur, (comme le confirme l'étude statique effectuée aux questions de la Partie A et de la Partie B). Le câble étant sans pertes (conducteurs parfaits, milieu assimilé au vide), on peut en donner la modélisation suivante :
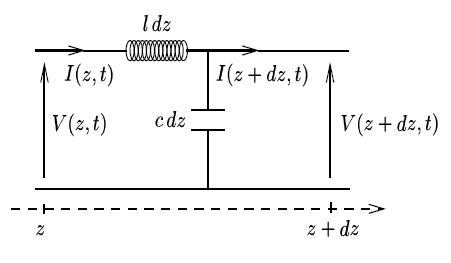
En utilisant la loi des mailles à l'instant
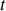sur la portion de circuit comprise entre
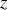et
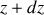, on obtient :
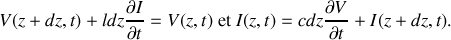
En d'autres termes :
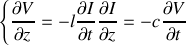
ce qui conduit à l'équation de propagation
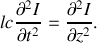
La relation précédente est communément appelée équation des télégraphistes. On obtient une équation analogue pour la tension
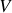. La solution générale de l'équation des télégraphistes se met sous la forme :
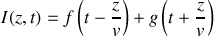avec
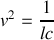
Le courant dans la ligne est donc la superposition de deux ondes progressives se propageant à la vitesse
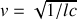, l'une selon les
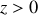et l'autre selon les
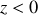. De même, pour la tension, on a :
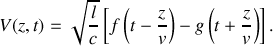
On définit l'impédance itérative de la ligne en étudiant le cas où l'onde ne se propage que selon les
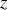croissants :
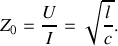
Dans notre modèle, la ligne est fermée en
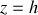par une résistance
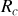. On a donc la relation
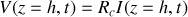. Cette dernière contrainte impose :
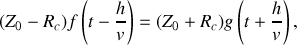
d'où l'expression du courant dans le câble :
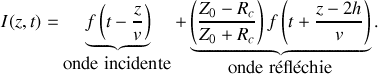
Le coefficient de réflexion de l'onde est alors :
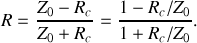
On constate que pour
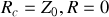, ce qui signifie qu'il n'y a pas d'onde réfléchie dans la ligne. La sortie de la ligne électrique est dite adaptée, puisque l'intégralité du signal entrant est transmis à la sortie de la ligne. On a, en reprenant les valeurs de
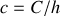et
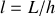, l'expression :
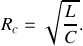
Les deux descriptions sont équivalentes du point de vue de la fermeture de la ligne par la résistance
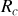. En effet, la forme proposée à la question de la partie C. pour l'onde électromagnétique se propageant dans le câble supposait l'absence d'onde réfléchie à la sortie.
