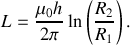Réponse 1
a
Nous pouvons avancer les mêmes explications qu'à la question 1.a de la partie A, pour justifier que le champ
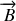ne dépend pas des variables
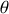et
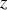, d'où
.
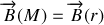La distribution de courants est symétrique par rapport à tout plan
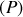contenant l'axe
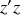du câble coaxial. Le champ d'induction magnétique
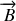est donc antisymétrique par rapport à ce plan
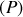. En particulier, en un point
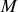du plan
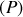, le champ est orthogonal à
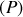. Le champ d'induction magnétique est donc, en tout point
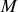de l'espace, de la forme
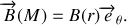
b
On applique le théorème d'AMPERE
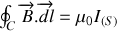
avec comme contour
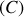un cercle de rayon
centré sur l'axe
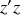, les différentes orientations étant reliées entre elles par la règle du tire-bouchon. Avec la forme de
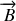donnée à la question précédente, il vient
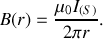
Il faut considérer trois régions d'espace :
1.
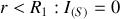
2.
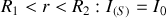
3.
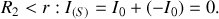
D'où :
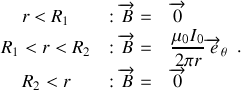
Réponse 2
L'énergie magnétique emmagasinée dans le câble peut s'écrire :
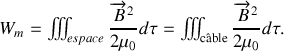
On utilise alors l'expression de
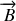calculée à la question précédente, les bornes d'intégration étant
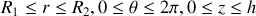. On obtient ainsi :
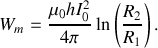
Or, du point de vue de la magnétostatique, le câble est un conducteur cylindrique de longueur
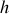. On peut définir son inductance propre
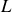par la relation
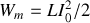. D'où l'expression de
:
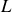