Réponse 1
En suivant les directives du texte, on remplace \varphi dans la formule de la température trouvée à la question A.2. par son expression trouvée en A.1. En évaluant la relation ainsi obtenue pour z=0 il vient :
T_S(t) = T_C - \left(\frac {\rho_gJ_g}{\lambda_g}\right)\, \left(l\frac {dl}{dt}\right).
Réponse 2
En effectuant exactement les mêmes opérations mais en utilisant cette fois comme expression pour \varphi, non plus le résultat de A.1., mais celui de A.2., on obtient une nouvelle expression de T_S.
T_S= T_C - \frac {h(T_s-T_a)l}{\lambda_g}\qquad \Leftrightarrow\qquad T_S(\lambda_g+hl) = \lambda_gT_C+ hlT_a
que l'on peut réécrire
T_S(t) = \frac {hlT_a+\lambda_gT_C}{\lambda_g+hl} .
Réponse 3
A partir des données de l'énoncé, il apparaît que
l_0 = \frac {\lambda_g}{h} est homogène à une longueur
Par conséquent, les deux termes qui apparaissent au dénominateur de l'équation précédente (\lambda_g et hl), sont de même dimension, comme il se doit... De même,
\tau est homogène à un temps.
Pour résoudre l'équation de l(t) on combine tout d'abord les résultats obtenus aux deux premières questions de cette partie, combinaison de laquelle ressort
T_C- \left(\frac{\rho_gL_h}{\lambda_g}\right) \,\,l\frac {dl}{dt} = \frac {T_a+ (l_0/l)T_C}{1+(l_0/l)
T_C - \left(\frac{\rho_gL_g}{\lambda_g}\right) \,\,l^2_0 \,\,\left(\frac{l}{l_0}\right) \frac {d(l/l_0)}{dt} = \frac {T_a+(l_0/l)T_C}{1+(l_0/l)}.
On cherche alors à réarranger le tout en faisant apparaître les longueurs et temps caractéristiques introduits par l'énoncé, ce qui débouche sur l'équation différentielle suivante :
\frac {2\tau}{l_0} \frac{dl}{dt} = \frac {1}{1+l/l_0}.
Pour la résoudre de la manière la plus simple possible, définissons les grandeurs sans dimension
L = \frac {l}{l_0}\quad et \quad T= \frac {t}{\tau}.
On se ramène ainsi à la résolution de
2\frac {dL}{dT} = \frac {1}{1+L'}
ce qui conduit à :
2\,(1+L)\, dL = dT
(1+L)^2\,=\,T+C^{te}.
Enfin, la condition initiale sur l se transpose à L pour donner
L(T=0) = 0\qquad \Rightarrow\qquad (1+L)^2= T+1
ce qui, en revenant aux variables dimensionnées, donne pour l'épaisseur de glace du lac
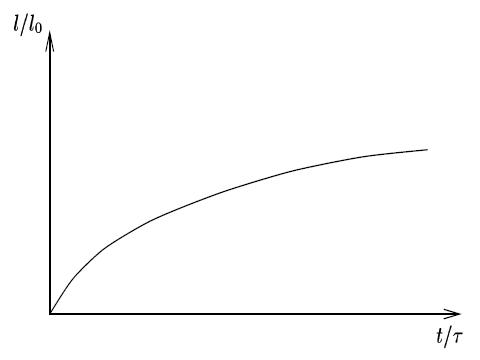
l(t) = l_0 \left(\sqrt{1+\frac {t}{\tau}-1}\right)
L'allure du graphe correspondant est représentée sur la figure 5. B.4.
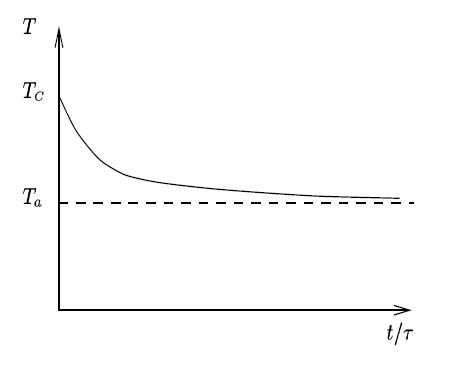
Pour trouver la relation donnant la température de la glace en surface, repartons du résultat de la question B.2., en y reportant la loi de variation de l en fonction du temps. On obtient
T_S = \frac {hlT_a+\lambda_gT_C}{\lambda_g+hl} = T_a+\frac {l_0}{l+l_0}(T_C-T_a),
ce qui donne finalement
T_S(t) = T_a + \frac {T_C-T_a}{\sqrt{1=t/\tau} .
A titre de vérification, on peut remarquer que cette formule se comporte dans les deux limites temps courts et temps longs, conformément à l'intuition. En effet t = 0, T_S pour est égale à la température de l'eau avec laquelle le contact thermique a été supposé parfait, alors que pour t\rightarrow+\infty ,cette même température de surface tend à s'équilibrer avec celle de l'air qui est à son contact. Cette décroissance vers la limite T_a se fait là encore suivant une loi en racine carrée ce qui nous donne l'allure suivante :