Définitions
Par définition nous appellerons système matériel un ensemble de points matériels. Nous distinguerons deux sortes de systèmes matériels :
Système matériel indéformable :
Tous les points matériels constituant le système restent fixes les uns par rapport aux autres. Ceci correspond à la définition d'un solide en mécanique.
Système matériel déformable :
Tous les systèmes ne correspondant pas à la définition d'un solide.
Exemple :
deux solides, sans liens entre eux, forment un système déformable lorsque chacun des solides se déplace indépendamment de l'autre.
Lorsqu'il ne subit aucune action venant de l'extérieur, un système matériel est dit isolé (ou fermé). C'est le cas d'un solide seul dans l'espace, loin de toute autre masse.
Si des actions extérieures agissant sur un système se compensent, alors on dit que le système est pseudo-isolé c'est à dire que tout se passe comme s'il était isolé.
Remarque :
Sur la Terre, il n'est pas possible de rencontrer des systèmes rigoureusement isolés. L'action de la Terre est une action extérieure pour tout système matériel. Par contre on peut rencontrer des systèmes pseudo-isolés chaque fois que l'action de la Terre est compensée. C'est le cas des mobiles auto-porteurs ou encore d'un système se trouvant sur une table soufflante. Dans ces cas, le coussin d'air compense l'action de la Terre et élimine les principales forces de frottements qui sont les frottements solide-solide. On retrouve la même situation sur une surface horizontale glissante comme la surface gelée d'une patinoire.
Attention :
Par la suite, par mesure de simplification, nous utiliserons le terme isolé pour tout système effectivement isolé ou pseudo-isolé.
Masse et centre d'inertie
La masse d'un système caractérise la quantité de matière qu'il renferme. Elle est invariable dans le cadre de la mécanique Newtonienne. C'est une caractéristique du système. Dans le système international d'unités, l'unité de masse est le kilogramme (kg).
Remarque :
Le centre d'inertie d'un système matériel (ou centre de gravitation) correspond au point noté
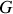barycentre des positions des points matériels affectés de leur masse. Par définition du barycentre, le point
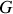vérifie
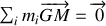
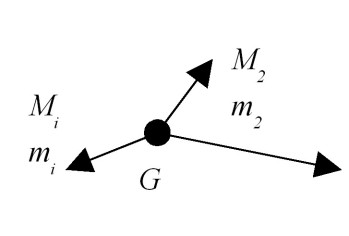
Pour un système discret constitué de
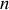masses
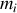situées aux points
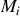on aura, par rapport à un point
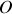origine :
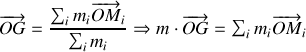
avec
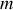= masse totale du système.
Si le système forme un milieu continu à l'échelle macroscopique, le signe somme se transforme en signe intégrale :
