Quel choix de référentiels ?
1) Le mouvement du centre de gravité de la Terre et des planètes du système solaires sont décrits dans un référentiel héliocentrique (
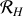) : ses axes pointent vers trois étoiles ‘fixes' et lointaines.
Les étoiles sont si éloignées du système solaire que le mouvement de la Terre et des autres planètes peut avoir lieu sans que les directions des axes de ce référentiel ne soient perturbées par le mouvement des étoiles (fig 11).
Pour les observations terrestres dont la durée est courte par rapport au mouvement annuel autour du Soleil, seule la rotation propre de la Terre peut être considérée (isolée).
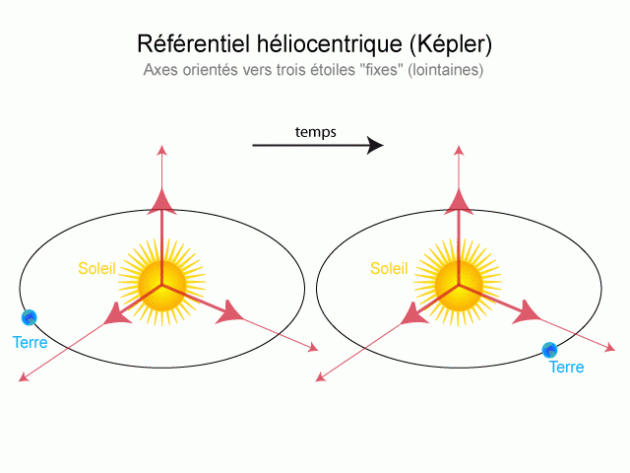
2) Pour cela, peut être choisi un second référentiel ‘fixe' de centre
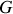noté
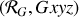, dont les axes sont parallèles à ceux du référentiel héliocentrique (en rouge sur la fig. 12). Ce dernier référentiel est considéré comme galiléen. C'est le référentiel géocentrique de Léonard.
La description des phénomènes dus à la rotation propre de la Terre est alors réalisée de manière simplifiée dans un référentiel mobile (
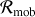) qui sera à préciser selon le mouvement et le phénomène à décrire.
La symétrie quasi sphérique de la Terre et les repérages à sa surface en
longitude (décrite selon le plan méridien par la variable
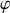) et latitude ( par rapport au plan 'équateur' et
)
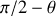incitent à l'utilisation de référentiels associés aux coordonnées sphériques (
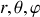) comme sur la fig. 12.
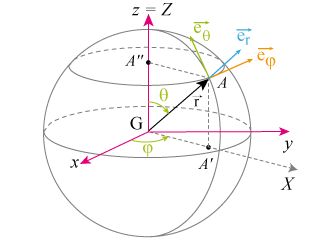
Mais avant de préciser les référentiels mobiles de la fig. 12 et leur utilisation pour les mesures terrestres, quelques remarques peuvent aider à comprendre les analyses et choix à venir.
Méthode : Quelques ordres de grandeur
Un point
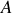(ou
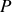pour Paris) à la surface de la Terre est repéré essentiellement par sa latitude
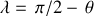(angle avec le plan de l'équateur ;
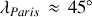). Sa longitude importe peu, relativement à la rotation propre de la Terre : du fait de la rotation terrestre, ce point va décrire un cercle autour de l'axe de rotation de rayon
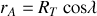avec la même vitesse de rotation que la Terre. Un référentiel tournant avec le plan méridien permet d'isoler l'effet de la rotation terrestre.
Quelques valeurs numériques dont
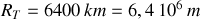et 
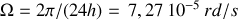soit
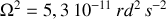.Elles permettent d'évaluer les ordres de grandeur des effets.
Ainsi à la surface de la terre, la vitesse linéaire due à la rotation de la terre est :
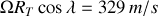soit près de
!!!
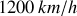Simplifications dues à la rotation de la Terre.
Dans un référentiel mobile, l'équation générale du mouvement est :
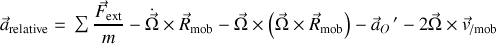
Dans le cas de référentiels terrestres, deux termes disparaissent puisque la vitesse de rotation est constante et que les référentiels mobiles sont fixés à la Terre.
Ne subsistent alors que les accélérations ‘centrifuge' et de Coriolis lesquelles, à première vue et en module, sont respectivement proportionnelles à
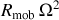et
.
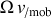La puissance en
suggère, au moins dans un premier temps, un traitement individuel de chaque terme.
Une approximation qui ne sera pas toujours valide puisqu'elle est tributaire des valeurs des grandeurs (
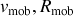) ainsi que des conditions initiales.
Un référentiel sera adapté à la description de chacune de ces deux accélérations.
Explication : 1) Accélération centripète et force d'inertie centrifuge
Un point
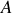, immobile à la surface de la Terre à la latitude
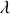tourne avec la Terre.
Il décrit dans le référentiel géocentrique un cercle dans le plan parallèle à l'équateur et va donc subir une pseudo-force centrifuge dans ce même plan.
Présenté ainsi, une représentation de type ‘coordonnées polaires' ou ‘cylindriques' est suffisante.
Dans ce cas de figure, simplifié, le référentiel mobile choisi est centré au centre de la Terre
.
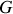Ses axes
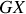et
sont dans le plan méridien
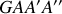et tournent à la vitesse de rotation de la Terre autour de
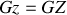, (verticaux sur la Fig 12 et confondus).
L'axe
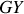est perpendiculaire au plan méridien.
Dans ce référentiel, les grandeurs qui apparaissent prennent la forme suivante :
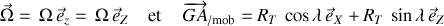
Une variante de ce référentiel est obtenue par une translation le long de l'axe
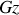du point
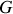vers le point
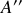selon
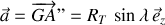. Ce référentiel est noté
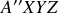, sa position dépend du point de mesure et le plan
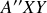est parallèle à l'équateur.
Ces référentiels possèdent des axes parallèles à ceux des coordonnées polaires.
Ils tournent autour de l'axe
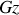avec la correspondance :
).
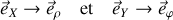L'expression de l'accélération centripète se simplifie alors :
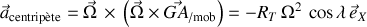
Elle correspond à la composante
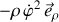des coordonnées polaires.
- La pseudo-force centrifuge obtenue avec (
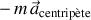) permet de réaliser, avec la force gravitationnelle dirigée vers le point
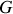, l'équilibre du fil à plomb : ceci modifie de quelques minutes d'angle la direction de la force de pesanteur.
- Par ailleurs, le module de cette pseudo-force est maximal pour
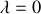(à l'équateur) et nul aux pôles : ceci explique la forme originelle non sphérique de la Terre.
Explication : 2) Accélération de Coriolis et pseudo force de Coriolis
Lorsqu'un mouvement a lieu à la surface de la terre, comme le lancement d'une fusée ou d'un engin balistique, c'est-à-dire sur de grandes distances ou avec de grandes vitesses relatives, un référentiel mobile peut être utilisé, équivalent de celui des coordonnées sphériques mais dont l'origine est à la surface de la Terre en
.
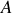L'axe
est radial de vecteur unitaire
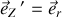des coordonnées sphériques ; il passe par le centre
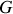de la terre.
Les deux autres axes
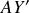et
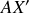sont situés dans le plan tangent à la surface de la Terre en
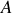et dirigés par exemple respectivement vers le Nord (
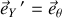) et l'Est (
).
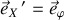Avec ces choix le repère est trirectangle direct.
Le vecteur-rotation de la Terre s'écrit :
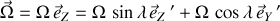
Si la vitesse du point matériel
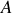est notée :
,
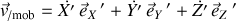l'accélération de Coriolis dont la forme générale est :
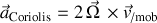
s'écrit :
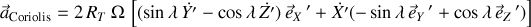
Ces
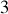composantes de l'accélération peuvent à priori donner
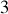composantes de la vitesse : ceci dépend des conditions initiales en vitesse.
Néanmoins, chacun peut noter que les lancers orientés vers l'est ou l'ouest ( selon
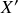) ont pour effet de dévier les trajectoires dans les
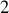autres directions, alors que les lancers vers le Sud ou le Nord (les valeurs des vitesses sont algébriques) ou vers la haute atmosphère radialement, (selon
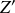), produiront des déviations vers l'Est ou l'Ouest.
Les applications spécifiques se déclinent à l'infini.
Attention : Et dans le cas d'un mouvement général.
Ce traitement séparé des deux composantes de l'accélération relative n'est pas rigoureux.
Il permet juste de visualiser les effets dominants en les différenciant.
Dans la réalité les équations du mouvement dans le référentiel mobile sont des équations différentielles du second ordre qu'il est nécessaire d'intégrer en tenant compte de toutes les composantes de l'accélération et surtout des conditions initiales en vitesse et position.
Dans le cas général, le référentiel mobile utilisé est celui
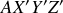, d'autant que la force extérieure est gravitationnelle, dirigée selon
(
).
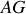La composante centrifuge n'est plus contenue dans le plan
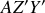puisque le point matériel étudié est en mouvement dans (
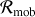), ses projections se déduisent de la forme générale de la source centripète :
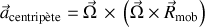où
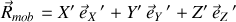
Pour surmonter la complexité des équations, l'ordre de grandeur de la vitesse de rotation terrestre ainsi que les valeurs des vitesses initiales permettent d'approcher des solutions par un développement limité.
Remarque : Référentiel fixe ou approximation.
L'ordre de grandeur d'un paramètre, comme la vitesse angulaire, permet de visualiser ou presque l'amplitude d'un phénomène.
De la même manière, la notion de référentiel ‘fixe', de fait inexistant dans la nature, constitue une approximation circonstanciée.
Ainsi dans notre univers en expansion, le déplacement du Soleil produirait un effet d'entraînement sur les planètes mais sur des échelles de temps adéquates et adaptées aux types de mesures effectuées.
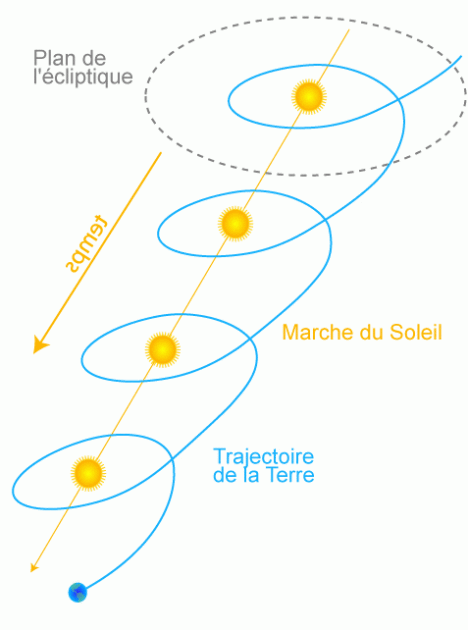
Sur la fig. 13 un mouvement composé de la Terre est représenté.
Le mouvement du soleil est schématisé comme rectiligne et mesurable sur une échelle de temps annuelle.
Il est à l'origine d'une composante d'entraînement dans le mouvement terrestre.
Néanmoins le référentiel géocentrique utilisé pour les applications typiquement terrestres peut être considéré comme fixe.
Il constitue une excellente approximation pour le type et surtout la durée des effets mesurés. L'influence de la mobilité de ce référentiel peut donc être négligée.
De même nul besoin de tenir compte du mouvement de la terre autour du soleil, ni même de sa rotation propre, pour mesurer la période d'un pendule plan : le référentiel du laboratoire suffit.
Mais sur une mesure de 24h, le pendule de Foucault, par une oscillation devenue conique, permet de mettre en évidence la rotation propre de la terre.
