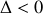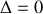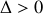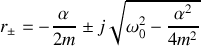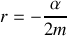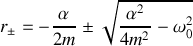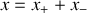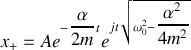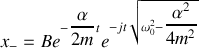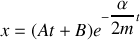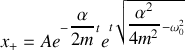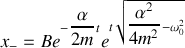Nous considérons un pendule élastique horizontal subissant une force de frottement visqueux du type
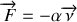. Nous étudions le système masse
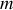dans le référentiel
.
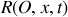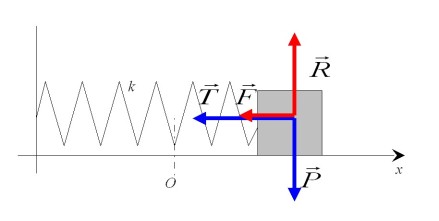
Les forces extérieures appliquées sont le poids
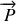, la force de frottement
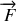; la tension du ressort
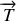et la réaction du support
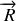. L'application de la R.F.D. conduit à:
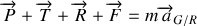
avec:
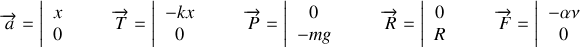
En projection sur l'axe des
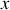il vient:
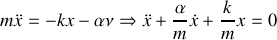
Cette équation est une équation différentielle linéaire du deuxième degré. Les solutions sont exponentielles car en effet il s'agit de trouver une fonction solution dont la dérivée seconde et première sont proportionnelles à la fonction elle-même. Nous considérons donc une solution du type:
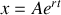
Le report de cette solution dans l'équation différentielle conduit à:
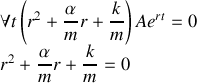
La dernière de ces équations s'appelle équation caractéristique de l'équation différentielle.
Remarque :
La résolution de l'équation caractéristique de l'équation différentielle permet de déterminer les solutions de l'équation différentielle dans les différents régimes d'amortissement. Comme il s'agit d'une équation du second degré, il importe de distinguer trois cas qui correspondent à la valeur positive, nulle ou négative du discriminant. Le discriminant de cette équation s'écrit en faisant apparaître la pulsation propre de l'oscillateur:
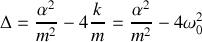
Nous présentons dans le tableau ci-dessous les trois cas qui sont donc à distinguer avec les solutions correspondantes de l'équation caractéristique et de l'équation différentielle :
Nous étudions tout d'abord le cas très fréquent de l'amortissement faible.
amortissement faible |
amortissement critique |
amortissement fort |
|
|
|
|
|
|
