Nous avons vu que la solution de l'équation différentielle s'écrit:
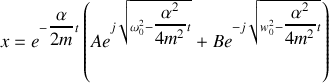
La somme des deux exponentielles complexes peut s'exprimer plus simplement par un cosinus ce qui conduit à:
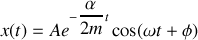
avec
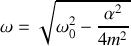
qui est la pulsation du mouvement. La position de l'oscillateur s'exprime donc par un produit de deux termes.
Le premier terme est une exponentielle décroissante et représente l'enveloppe du mouvement de l'oscillateur c'est à dire les positions extrémales prises par
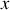lorsque le temps s'écoule. La décroissance de l'exponentielle est guidée par le rapport
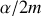qui traduit l'amortissement plus ou moins prononcé du mouvement. Lorsque
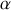est nul le mouvement est non amorti et l'on retombe sur le cas de l'oscillateur harmonique non amorti.Le second terme est un cosinus qui traduirait la périodicité du mouvement s'il n'y avait pas d'amortissement. Comme la période du mouvement de l'oscillateur dépend de l'amortissement et de ce fait diffère de la période propre de l'oscillateur on parle de pseudopériode et l'on dit que le mouvement est pseudopériodique .
Remarque :
Bien que le mouvement n'est plus périodique puisqu'au bout du temps
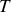l'élongation de l'oscillateur ne reprend pas la même valeur donc
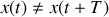. La pseudopériode est donnée par:
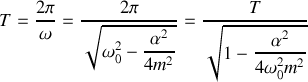
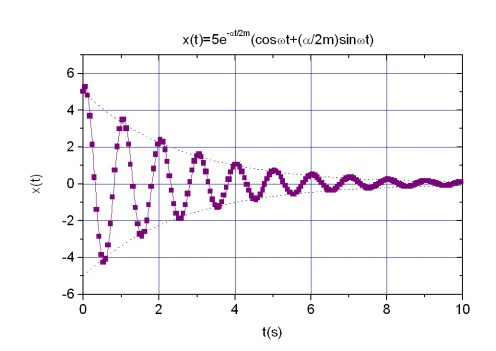
Cette expression montre que la période de l'oscillateur amorti augmente avec l'amortissement. Nous pouvons donc affirmer que les frottements ralentissent le mouvement. La figure 8 montre l'évolution de l'élongation
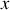du ressort pour un pendule élastique amorti par frottement visqueux.
Remarque :
Les constantes
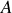et
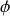sont déterminées par les conditions initiales du mouvement qui généralement sont
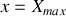et
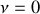à
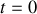, ce qui conduit à:
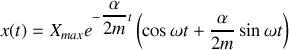
Dans la pratique, il existe deux solutions pour réaliser l'amortissement visqueux.
La première consiste à utiliser un pendule élastique horizontal monté sur coussin d'air et à accrocher à la masse
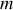une palette verticale trempant dans un liquide.La seconde consiste à amortir le mouvement d'un pendule élastique vertical par une force de Lorentz en plongeant la masse
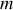dans un champ magnétique
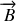uniforme.
On démontre que les courants induits dans la masse produisent une force de freinage opposée à la vitesse de déplacement de la masse.
Remarque :
La détermination du coefficient de viscosité
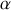peut se faire expérimentalement à partir de la courbe
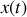en utilisant le
décrément logarithmique
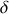. Cette quantité est obtenue en considérant le logarithme du rapport des amplitudes des oscillations au bout des temps
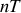et
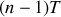. A ces instants nous avons:
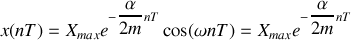
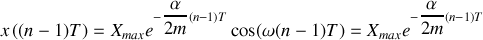
Complément :
Le décrément logarithmique qui est le logarithme du rapport des amplitudes est donné par:
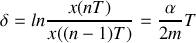
Cette quantité est facilement accessible par l'expérience et permet de déterminer rapidement
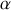. Une méthode plus précise consiste à tracer le logarithme de l'amplitude
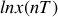en fonction de
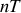. On obtient alors une droite de pente
.
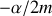