Remarque :
Le régime de l'oscillateur est dit critique lorsque le discriminant de l'équation caractéristique est nul. Dans ce cas le mouvement de l'oscillateur obéit à une équation horaire du type:
Attention :
Le régime est dit critique car il correspond à un amortissement critique pour lequel on bascule du régime pseudopériodique vers un régime ou il n'y a plus d'oscillations.
Les constantes
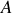et
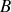sont déterminées par les conditions initiales du mouvement. qui sont supposées être
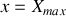et
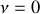à
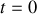. L'introduction de ces deux conditions conduit à une solution du type:
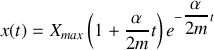
Remarque :
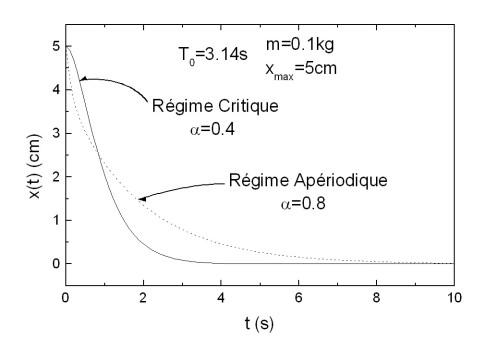
Dans la pratique, ce régime est extrêmement important car lorsqu'il est atteint, l'oscillateur revient dans sa position d'équilibre au bout d'un temps minimal. C'est ainsi que ce régime est mis à profit dans les systèmes d'amortisseurs qui ont pour but d'empêcher les oscillations d'un oscillateur.
La figure 9 montre le retour à l'équilibre d'un ressort amorti en régime critique. La période propre d'oscillation est de
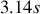et le retour à l'équilibre est de l'ordre de cette valeur.
