Comme annoncé dans l'introduction de ce cours, il s'agit ici d'étudier le comportement d'un solide dans le domaine élastique des déformations (réversibilité et linéarité). Dans ces conditions, il existe une relation linéaire entre contraintes et déformations pures. Il s'agit de la loi de Hooke :

où sont les éléments du tenseur des contraintes , les éléments du tenseur des déformations pures , et les éléments du tenseur de rigidité . Compte tenu du fait que et sont des tenseurs de rang 2, est nécessairement un tenseur de rang 4 comportant éléments. Notons qu'une relation inverse peut s'établir de manière équivalente en exprimant les déformations en fonction des contraintes à l'aide d'un tenseur de rang 4 appelé tenseur d'élasticité.

et étant symétriques, le tenseur de rigidité (ou celui d'élasticité) est nécessairement symétrique en i et j, ainsi qu'en k et l. Le nombre d'éléments indépendants composant est donc ramené de 81 à 36. Ce nombre d'éléments reste élevé mais peut encore être restreint en considérant la symétrie du matériau étudié : une ultime simplification consiste à considérer un matériau isotrope. Dans ce cas, le nombre d'éléments indépendants constituant est ramené de 36 à 2, se limitant donc aux coefficients élastiques de Lamé et . Cela signifie que le comportement élastique d'un matériau isotrope est complètement défini à partir de la connaissance de ces deux seuls paramètres. Ainsi, chacun des éléments de peut se formuler en fonction des coefficients élastiques de Lamé :

où est le symbole de Krönecker.

Il en résulte que la loi de Hooke se réécrit :

Cette nouvelle formulation peut se simplifier en remarquant notamment que le symbole de Krönecker force l'égalité des indices dans une sommation : . On obtient ainsi :

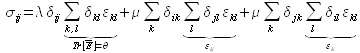
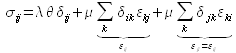
et finalement : , ou de façon équivalente . Cette dernière formulation correspond donc à la loi de Hooke appliquée au cas d'un matériau élastique isotrope.