Les deux coefficients de Lamé, 
et 
, sont des paramètres caractérisant les propriétés élastiques du matériau mais ne sont pas directement accessibles par mesure expérimentale. Il existe néanmoins deux autres paramètres, caractérisant pareillement les propriétés élastiques du matériau, qui s'obtiennent expérimentalement à partir d'une mesure simple : il s'agit du module d'Young E et du coefficient de Poisson 
. Cette partie a donc pour objectif de présenter la mesure de ces deux paramètres et d'établir leur lien avec les deux coefficients de Lamé.
Comme le montre la figure 20, l'expérience consiste à soumettre une éprouvette de longueur 
et de section 
à une traction longitudinale.
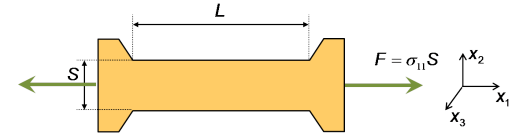
Cette traction résulte d'une force exercée par unité de surface 
et est proportionnelle à l'allongement relatif mesurable dans la direction longitudinale repérée par 
. Le coefficient de proportionnalité correspond au module d'Young et se formule donc :
Cette traction engendre naturellement d'autres déformations qu'il convient d'expliciter en appliquant la loi de Hooke :
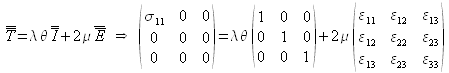
ce qui conduit, par identification, aux relations suivantes :
(i)
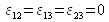
(ii)
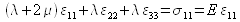
(iii)
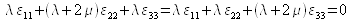
La relation (i) permet de constater qu'il y a absence de glissement (pas de déformations angulaires pures dans le repère choisi). Par conséquent, seuls les allongements relatifs 
sont à considérés. La relation (iii), après simplification, conduit à 
: les allongements relatifs dans la direction transverse sont identiques. En remplaçant
par 
dans la relation (ii), on obtient alors 
, nouvelle relation permettant d'établir une proportionnalité entre 
(ou 
) et 
:
Ce coefficient de proportionnalité, négatif, définit le coefficient de Poisson 
et permet de formuler :
On peut donc en conclure que module d'Young et coefficient de Poisson sont deux paramètres, propriétés intrinsèques du matériau, que l'on peut facilement déterminer expérimentalement par la mesure des allongements relatifs longitudinal (
) et transversal (
).
Remarque :
Le parti pris d'un coefficient de Poisson positif implique une formulation 
où le signe moins est en cohérence avec le fait logique qu'une traction longitudinale (
) génère une contraction transversale (
).
Établissons maintenant un lien direct entre les coefficients de Lamé et le module d'Young ainsi que le coefficient de Poisson. Reprenons la relation (iii) et remplaçons 
et 
par 
: 
, ce qui conduit à :
Faisons de même dans la relation (ii) : 
. On obtient alors :
soit :
Il est ensuite facile de retrouver les relations inverses permettant d'exprimer les deux coefficients de Lamé en fonction de 
et 
:
Remarque :
Les différentes grandeurs impliquées jusque là ont des dimensions qu'il convient de rappeler ou déterminer :
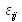est un allongement relatif (sans dimension) ou un glissement (déformation angulaire pure, sans dimension) ; par conséquent, il s'agit d'une grandeur sans dimension, pouvant être positive ou négative.
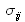est une contrainte (tension, compression ou cisaillement) ; correspondant à une force par unité de surface, sa dimension est celle d'une pression (exprimée en Pa) pouvant être positive ou négative.Les deux coefficients de Lamé
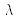et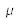 
ont nécessairement la même dimension que 
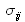, ce qui découle de l'homogénéité de la loi de Hooke 
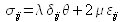; ils s'expriment donc en Pa et ont la dimension d'une pression. Ils sont par ailleurs positifs (ce qui peut être facilement démontré à partir des relations précédemment établies).Le module d'Young est défini expérimentalement à partir de
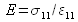, établissant d'une part que sa dimension est celle d'une contrainte (en Pa) et d'autre part que sa valeur est nécessairement positive (une traction génère un allongement ou bien une compression génère un rétrécissement, l'allongement relatif étant nécessairement de même signe que la contrainte).Le coefficient de Poisson est défini comme l'opposé du rapport de l'allongement relatif transversal sur l'allongement relatif longitudinal (
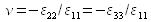) ; il en résulte que ce coefficient est sans dimension et, qu'ainsi défini, il est nécessairement positif. En outre, la formulation de 
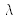en fonction de 
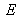et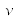 
permet de montrer que 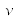est nécessairement inférieur à ½. Quel que soit le matériau envisagé, on a donc 
.
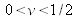