Un certain nombre d'autres grandeurs sont courant utilisées dans l'analyse des propriétés mécaniques des matériaux. Nous n'en ferons pas ici une liste exhaustive mais déclinerons certaines d'entre elles en partant de la forme tensorielle de la loi de Hooke : .

Décomposons les tenseurs des contraintes et des déformations pures en séparant partie sphérique et déviateur :

Par identification, on en déduit :

• (i)

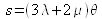
• (ii)

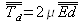
En posant , on définit à partir de la relation (i) le module de rigidité à la compression , lequel correspond en pratique à l'inverse du coefficient de compressibilité puisque : . Par ailleurs, on peut reformuler sans difficulté le module de rigidité à la compression en fonction du module d'Young et du coefficient de Poisson : .

La relation (ii) rend proportionnels les deux déviateurs. Le coefficient de proportionnalité correspond au double du deuxième coefficient de Lamé , lequel porte logiquement l'appellation de module de rigidité au glissement (ou module de Coulomb).

La relation réciproque de la loi de Hooke permet d'exprimer les déformations pures en fonction des contraintes :

Introduisons le module d'Young et le coefficient de Poisson en remarquant que d'une part et que d'autre part , ce qui conduit à . Par ailleurs, puisque , on a , d'où :

Ces relations entre les tenseurs se traduisent explicitement sur les vecteurs contrainte et déformation. Il s'agit simplement de multiplier scalairement la relation tensorielle par la normale à la facette étudiée :

Et puisque et , on obtient :

Dans le repère lié à la facette, défini par , les composantes de la contrainte s'expriment alors :

où apparaissent les expressions de l'allongement relatif et du glissement .

Il en résulte :