Dans le cadre de la mécanique analytique, les principales équations qui permettent d’analyser le mouvement sont brièvement décrites ci-dessous.

Le système limité à l’électron dans son mouvement autour du proton, est caractérisé par la fonction de Hamilton associée à l’énergie totale et qui s’exprime en fonction des coordonnées et impulsions généralisées :

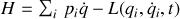
Avec la fonction de Lagrange définie par :

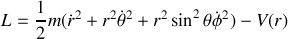
A partir de cette expression, on peut définir les impulsions généralisées sous la forme :

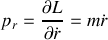
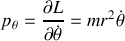
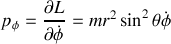
Et enfin, la fonction de Hamilton du système peut se mettre sous l'expression ci-dessous :

- En fonction des coordonnées et vitesses généralisées

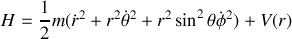
- En fonction des coordonnées et impulsions généralisées

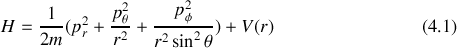
Et s'identifie donc à l'énergie totale du système.

Equations du mouvement de Hamilton

Ces équations permettent de traiter le mouvement au même titre que la relation fondamentale de la dynamique. Une écriture simple des équations dites « canoniques » est la suivante :

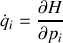
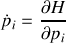
et se développent en coordonnées sphériques selon les 6 relations ci-dessous :

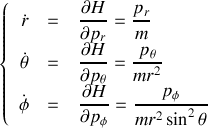et

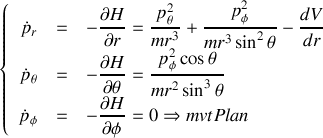
Dans le cas d'un mouvement dans un potentiel central, le mouvement est plan et par un choix des conditions initiales telles que 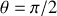, on simplifie les relations ci-dessus et l'équation de la trajectoire peut être obtenue en intégrant l'équation différentielle :

En fonction des caractéristiques du mouvement cette équation permet de décrire le mouvement au même titre que la mécanique newtonienne. Cependant, l'avantage de la mécanique analytique (Lagrange, Hamilton) est d'introduire des grandeurs qui seront exploitées ultérieurement dans la nouvelle théorie quantique.