Imaginons un observateur O qui est arrivé à élaborer les « lois de la nature » en les exprimant sous forme d'équations mathématiques reliant entre elles des grandeurs physiques. Il s'agit par exemple des lois de Newton en mécanique, des équations de Maxwell en électromagnétisme. Prenons ensuite un autre observateur, O', qui étudie les mêmes phénomènes. Quelle sera sa description des « lois de la nature » ?
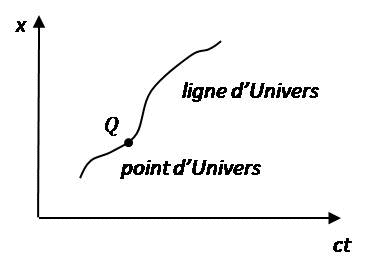
O et O' effectuent tous les deux des mesures, dans l'espace et dans le temps, ils vont donc se munir d'un système de coordonnées et d'une horloge. L'entité physique de base utilisée pour repérer un phénomène est appelée évènement. Un évènement associé à une particule matérielle Q peut être caractérisé par la donnée de la coordonnée temporelle t et des coordonnées de position, par exemple x,y,z (coordonnées cartésiennes) : on va naturellement travailler dans un espace à quatre dimensions avec un quadrivecteur position x^i,i=0-3, défini par la relation (x^0,x^1,x^2,x^3 )=(ct,x,y,z), où c est la vitesse de la lumière dans le vide. Dans cet espace, Q est appelé point d'Univers et la courbe qu'il décrit est appelée ligne d'Univers.
Supposons maintenant que l'observateur O utilise un référentiel R pour repérer les coordonnées d'un évènement, alors que l'observateur O' utilise un référentiel R' pour repérer le même évènement. On doit donc comparer ce que voit O au point (ct,x,y,z) avec ce que O' appelle le point (ct',x',y',z'). On se pose donc le problème de comparer des phénomènes rapportés à deux référentiels liés entre eux par une translation et/ou une rotation. Les « lois de la nature » préservent-elles l'invariance de forme des relations entre grandeurs physiques sous l'effet d'une translation et/ou d'une rotation ? Beaucoup de physiciens et de mathématiciens ont contribué à répondre à cette question, jusqu'à Einstein qui en a tiré les premières conséquences physiques.
-
1687 : Newton publie « Philosophiae naturalis principia mathematica », un traité de mécanique classique. Les équations de Newton sont invariantes par transformations de Galilée (changement de référentiel inertiel).
-
1873 : Maxwell finalise sa théorie sur l'électromagnétisme. Les équations de Maxwell ne sont pas invariantes par transformations de Galilée.
-
1887 : Expérience de Michelson-Morley : la vitesse de la lumière semble invariante par rapport à un changement de référentiel.
-
1895-1899 : Lorentz et Poincaré obtiennent des transformations qui laissent les équations de Maxwell invariantes dans tout référentiel inertiel.
-
1905 : Einstein publie deux articles « On the Electrodynamics of Moving Bodies » et «Does the Inertia of a Body Depend upon Its Energy-content». La théorie de la relativité restreinte est développée sur la base de deux postulats. Il obtient E=mc^2. Il a 26 ans ... Il devance Poincaré.
-
1908 : Minkowski publie un article important sur la structure métrique de l'espace-temps à 4 dimensions.
-
1915 : Einstein soumet pour publication l'article « The Field Equations of Gravitation ». Il y développe la théorie de la relativité générale. Hilbert le devance de 5 jours, mais ne revendiquera jamais la priorité de publication.