Pour les phénomènes de mécanique classique, le problème posé ci-dessus de l' l'invariance de forme des relations entre grandeurs physiques avait été formulé par les fondateurs de la mécanique classique, en particulier Newton.
-
La première loi de Newton postule qu'il existe un référentiel inertiel \mathcal{R}. Dans un tel référentiel, un mobile qui n'est soumis à aucune force extérieure se meut d'un mouvement rectiligne et uniforme (m\vec a=0 donc la vitesse \vec v est constante).
-
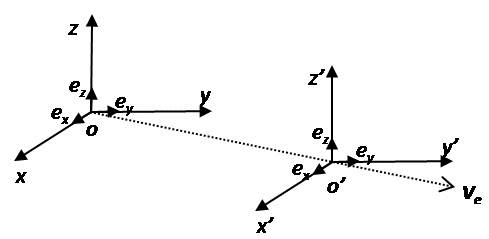
Il existe une infinité de référentiels inertiels. Tout référentiel spatial \mathcalR' qui se meut par rapport au précédent d'un mouvement rectiligne et uniforme, à la vitesse \vec V_e, est aussi un référentiel inertiel.
-
Les coordonnées d'un événement repéré dans \mathcal{R} et dans \mathcal{R}' sont reliées par la transformation de Galilée. Si on suppose que les origines o et o' des deux référentiels coïncident en t=t'=0, et que \vec V_e est la vitesse d'entraînement constante de \mathcal{R}' par rapport à \mathcal{R}, alors :
\vec {r'}=\vec r-\vec V_e t
c'est-à-dire :
-
x'=x-V_{ex} t
-
y'=y-V_{ey} t
-
z'=z-V_{ez} t
et t'=t
-
En dérivant la relation \vec {r'}=\vec r-\vec V_e t on obtient la loi d'addition des vitesses de la mécanique classique,
\vec v' = \vec v - \vec V_e \Leftrightarrow \vec v_{\mathcal{R}} = \vec v_{\mathcal{R}'} + \vec V_e
Clairement, si m \frac{d^2\vec r}{d t^2} = 0, alors m \frac{d^2\vec r'}{d t'^2} = m \frac{d^2\vec r'}{dt^2} = 0.
Si on admet l'invariance de transformation des forces, alors l'équation de Newton m\vec a = \vec F implique m\vec a' = \vec F'.
Cela signifie que les lois de la mécanique classique sont invariantes pour les transformations de Galilée : elles ont la même forme pour tous les observateurs inertiels.
C'est pourquoi il est impossible de détecter un mouvement rectiligne et uniforme d'un référentiel par des mesures faites dans ce référentiel («sans regarder par la fenêtre»). Le postulat de la relativité galiléenne dit que «les expériences faites à l'intérieur d'un laboratoire d'inertie ne permettent pas de déceler la vitesse relative de ces laboratoires».
Notons que dans la transformation de Galilée, tous les observateurs mesurent le même temps « absolu ». Par contre les coordonnées spatiales dans \mathcal{R}' dépendent à la fois des coordonnées spatiales dans \mathcal{R} et du temps. Que valent alors la durée galiléenne et la distance galiléenne entre deux évènements, repérés à la fois dans \mathcal{R} et \mathcal{R}' ?
Raisonnons sur un exemple.
Considérons le dispositif constitué d'une source lumineuse (situé au point o') d'un miroir (situé à une distance l de o' sur l'axe y'), attaché au référentiel \mathcal{R}'. La vitesse d'entraînement de \mathcal{R}' par rapport à \mathcal{R} vaut \vec V = V_{ex}\vec e_x (voir figure 3).
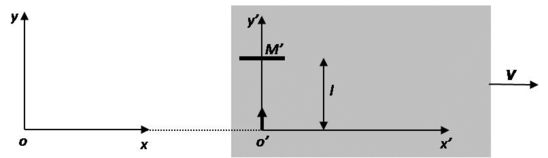
On appelle E_1 l'évènement « émission de lumière en o' en t = t' = 0 », E_2 l'évènement « réflexion sur le miroir plan M'» et E_3 l'évènement «détection en o' de la lumière réfléchie par M'». La lumière se propage à la vitesse c. Les coordonnées de ces évènements dans \mathcal{R}' valent :
\displaystyle{ E_1 \left\{\begin{array}{c c c c} x' = 0\\ y' = 0\\ z' = 0\\ t' = 0 \end{array} \qquad \displaystyle{ E_2 \left\{\begin{array}{c c c c} x' = 0 \\ y' = 0 \\ z' = 0 \\ t' = l/c \end{array}\qquad \displaystyle{ E_3 \left\{\begin{array}{c c c c} x' = 0 \\ y' = 0 \\ z' = 0 \\ t' = 2 l/c \end{array}
On applique la transformation de Galilée (éq. \vecr' = \vec r - \vec V_e t et t' = t ) pour obtenir les coordonnées de ces évènements dans \mathcal{R} :
\displaystyle{ E_1 \left\{\begin{array}{c c c c} x = 0 \\ x = 0 \\ z = 0 \\ t = 0 \end{array}\qquad \displaystyle{ E_2 \left\{\begin{array}{c c c c} x = V_{ex}t \\ y = l \\ z = 0 \\ t = l/c \end{array}\qquad\displaystyle{ E_3 \left\{\begin{array}{c c c c} x = V_{ex}t \\ y = 0 \\ z = 0 \\ t = 2 l/c \end{array}
La durée galiléenne entre les évènements E_1 et E_2 vaut \Deltat' = \Delta t = l / c, et entre les évènements E_1 et E_3 elle vaut \Deltat' = \Deltat = 2l/c. La durée galiléenne entre deux évènements est invariante par rapport au changement de référentiel (\Deltat' = \Deltat).
Par contre la distance galiléenne entre les évènements E_1 et E_2 vaut \Deltad' = l dans \mathcal{R}' et vaut \Delta d =(\frac{v_{ex}^2l^2}{c^2} + l^2)^{\frac12} dans \mathcal{R}. La distance galiléenne entre deux évènements n'est pas invariante par rapport au changement de référentiel (\Delta d \ne \Delta d').