Dans l'expérience imaginaire d'Einstein, on considère l'évènement E_1 « émission de lumière en o' en t = t' = 0» et l'évènement E_3 « détection en o' de la lumière réfléchie par M'». Pour l'observateur lié au référentiel \mathcal{R}', les coordonnées de ces évènements sont, comme précédemment (section 2.2) :
\displaystyle{ E_1 = \left\{ \begin{array}{c c c c} x' = 0 \\ y' = 0 \\ z' = 0 \\ t' = 0 \end{array} \qquad \displaystyle{ E_3 = \left\{ \begin{array}{c c c c} x' = 0 \\ y' = 0 \\ z' = 0 \\ t' = 2l/c \end{array}
Quant à l'observateur lié au référentiel \mathcal{R}, il voit le dispositif s'éloigner vers la droite à la vitesse \vec V_e = V_{ex}\vec e_x. A l'aide de son chronomètre il va mesurer un intervalle de temps \Deltat = t_3 - t_1 entre les évènements E_1 et E_3. De plus il décrira le trajet suivi par une impulsion lumineuse comme schématisé sur la figure ci-après :
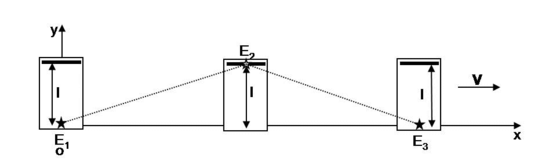
L'impulsion lumineuse suit le trajet \Delta E = E_1 \to E_2 \to E_3 (Pythagore) :
\Delta E = 2 \sqrt{l^2 + (\frac{1}{2} V_{ex}\Deltat)^2}
Par ailleurs O étant un observateur situé dans un référentiel inertiel, la vitesse de la lumière par rapport à O est égale à c, et donc la distance parcourue par celle-ci pendant l'intervalle de temps \Deltat vaut :
\Delta E = c \Deltat
En égalant les expressions \Delta E = 2 \sqrt{l^2 + (\frac{1}{2} V_{ex}\Deltat)^2} et \Delta E = c \Deltat, on obtient :
\Delta t = \frac{\frac{2l}{c}}{\sqrt{1 - \frac{V_{ex}^2}{c^2}}} = \frac{1}{\sqrt{1 - \frac{V_{ex}^2}{c^2}}}\Deltat' > \Delta t'
Ce résultat peut paraître paradoxal d'après notre « bon sens », il est toutefois parfaitement objectif : il n'y a pas de temps absolu. Einstein remet donc en cause l'invariance de la durée galiléenne par rapport au changement de référentiel : \Delta t \ne \Delta t'.
On utilise souvent les notations suivantes :
\beta_e \equiv \frac{V_{ex}}c
\gamma_e \equiv \frac{1}{\sqrt{1 - \beta_e^2}}
On remarque que lorsque ∣\beta_e∣ passe de 0 à 1, \gamma_e varie entre 1 et l'infini. Aussi la racine carrée implique que est une vitesse limite.
Dans le référentiel \mathcal{R}, les évènements E_1 et E_3 sont localisés au même point o'. Par définition, on appelle l'intervalle de temps associé \Deltat' durée propre (ou - abusivement - temps propre). L'équation \Delta t = \frac{\frac{2l}{c}}{\sqrt{1 - \frac{V_{ex}^2}{c^2}}} = \frac{1}{\sqrt{1 - \frac{V_{ex}^2}{c^2}}}\Deltat' > \Delta t' indique que l'intervalle de temps propre entre deux évènements est plus court que tout autre intervalle de temps, mesuré par un autre observateur inertiel. C'est aussi un pur effet de la géométrie de l'espace-temps (dans un triangle rectangle, le côté de l'angle droit est inférieur à l'hypothénuse) et de la constante c. Cette notion de durée propre sera formalisée mathématiquement à la section 5.1.