On remarque cependant, si on fait un bilan énergétique précis dans un transformateur, que les gains en champ dûs à la présence d'un matériau ferromagnétique à la perméabilité relative élevée sont accompagnés d'un échauffement de ce même matériau et de pertes énergétiques.
Ainsi, dans la partie excitatrice du système, en l'absence d'induit, on a lors d'une unité de temps
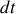
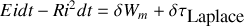
Les termes de gauche de l'équation représentent le travail fourni par le générateur de force électromotrice
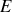et les pertes par effet Joule dans les fils d'alimentation de résistance
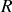parcourus par un courant
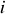, les termes de droite, respectivement l'énergie du champ magnétique et le travail des forces de Laplace (nul si le système est immobile), plus éventuellement un terme lié à la magnétostriction du matériau (modification de son volume due à la présence du champ magnétique suite à des effets à l'échelle atomique), que nous supposerons nul ici.
Rappel :
La densité volumique de puissance liée à un champ électromagnétique vaut
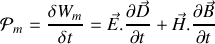
ce qui se simplifie ici vu l'absence de polarisation électrique.
Ce résultat peut être retrouvé en écrivant l'équation de l'induction dans le circuit :
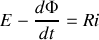avec
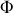le flux du champ magnétique.
par conséquent
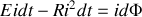
Si nous supposons que les lignes du champ magnétique sont circulaires et de longueur
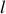, le théorème d'Ampère appliqué sur une ligne de champ à la surface externe du bâti donne
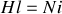
avec
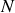le nombre de spires contenues dans la ligne de champ.
Par conséquent :
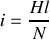
et si nous faisons l'approximation, pour un bâti du transformateur de faible épaisseur et de surface
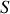, que le flux total vaut
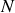fois le flux parcourant une spire
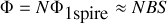
avec
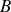le champ magnétique.
Alors
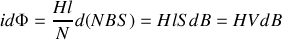
avec
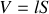volume du transformateur.
comme
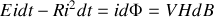
et
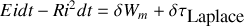
par unité de volume l'énergie magnétique a donc la même expression (
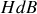) que le résultat établi en général.
Sur un cycle d'hystérésis l'énergie volumique fournie au matériau vaut donc
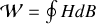
or
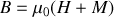
donc
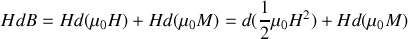
Attention :
Le premier terme du membre de droite représente l'énergie d'établissement du champ dans le vide et disparaît par parité pour un cycle symétrique. Le second terme représente l'énergie d'aimantation du milieu.
Ainsi :
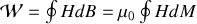
Mais le premier principe nous dit que la variation d'énergie interne du système sur un cycle doit être nulle. Par conséquent si
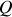est la quantité de chaleur échangée avec l'extérieur
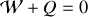
donc
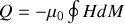
usuellement cette quantité de chaleur est négative donc on a échauffement du matériau (on peut aussi avoir refroidissement par démagnétisation).
Remarque :
Cette énergie dissipée sous forme de chaleur est issue d'un effet magnétique et non d'un effet Joule.
