En adoptant la démarche suivie par J.C. Maxwell , nous pouvons affirmer que la lumière est une onde électromagnétique caractérisée par l'association d'un champ électrique
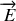, d'un champ magnétique
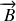et d'un vecteur d'onde
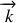. Cette affirmation nécessite évidemment d'être vérifiée. En particulier l'un des buts d'un cours d'optique physique est de montrer que la lumière est bien une onde. Pour cela nous allons tout d'abord l'admettre puis ensuite nous décrirons un ensemble d'expériences qui, nous le verrons, ne peuvent s'interpréter que par la nature ondulatoire de la lumière.
Dans le vide les champs
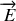et
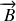qui définissent l'onde électromagnétique doivent satisfaire les quatre équations de Maxwell (1860)
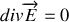
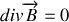
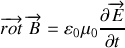
Lorsqu'elles sont combinées entre elles, ces équations conduisent aux équations de propagation du champ électrique ou magnétique qui s'écrivent :
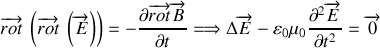
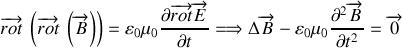
Rappel :
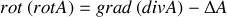
Le grand mérite des équations de Maxwell provient de ce que leur combinaison conduit aux équations de propagation, encore appelées équations de Helmoltz, et que ces équations nous indiquent que la propagation des champs électriques et magnétiques doit se faire à la célérité
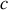vérifiant
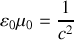. Les constantes
,
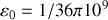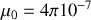étaient connues bien avant que Maxwell n'établissent ses équations. De ce fait, un simple calcul permit de vérifier que la célérité de propagation devait être
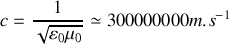
Remarque :
La valeur particulièrement grande de cette célérité correspond à peu de chose près à celle de la lumière dans le vide ainsi qu'elle avait été mesurée en premier lieu par Fizeau en 1849,
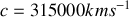, (par la méthode de la roue dentée) puis par Foucault en 1862 (par la méthode du miroir tournant),
.
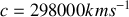Rappel :
Alors que Maxwell avait établi sa théorie sur des bases mécanistiques, c'est à Hertz que l'on doit rendre hommage car il fût le premier à proposer que la théorie électromagnétique de Maxwell s'appliquait parfaitement à la lumière pour peu que l'on considère la lumière comme une onde électromagnétique. La célérité de la lumière est une constante universelle et peut être mesurée en déterminant le temps mis par la lumière pour parcourir un mètre dans le vide. On trouve actuellement que
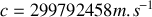
On peut percevoir dans l'analogie formelle des deux équations de propagation le rôle similaire joué par le champ
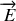et le champ
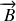. Cependant en optique les phénomènes physiques sont plutôt liés au champ électrique et on se contente en général d'utiliser le champ électrique
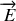pour décrire l'onde lumineuse. En effet les milieux magnétiques ne sont pas transparents et on appliquera les équations de Maxwell à la propagation dans des milieux diélectriques non magnétiques dans lesquels la densité de charge électrique est nulle et où il n'existe que des courants de déplacement (Voir cours électromagnétisme). Le cas des métaux est le seul cas ou les courants de conduction seront pris en compte.
Remarque :
La connaissance du champ électrique entraîne nécessairement celle du champ magnétique au travers des équations de Maxwell. La résolution de ces équations montre que les trois vecteurs
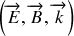forment un trièdre direct et que les champs
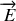et
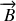peuvent présenter différentes formes selon la symétrie de la source qui les a produits.
Fondamental :
En particulier on distingue dans la pratique deux formes d'ondes très importantes : l'onde plane monochromatique et l'onde sphérique monochromatique qui sont des solutions simples de l'équation de propagation. Ces solutions sont pour l'onde plane et l'onde sphérique respectivement de la forme
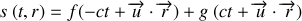
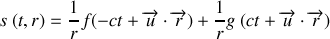
ou
désigne la distance du point
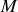d'observation à la source
,
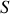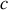est la célérité de propagation dans le milieu considéré et
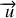est un vecteur unitaire dans la direction de propagation de l'onde. Les fonctions
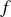correspondent aux ondes progressives alors que les fonctions
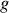décrivent les ondes régressives.
D'une façon très générale les solutions des équations de propagation seront de ce type et les fonctions
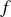et
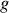seront déterminées par les propriétés de la source.
