Si l'on veut appréhender correctement la notion d'intensité lumineuse il importe de remarquer qu'une onde électromagnétique véhicule de l'énergie. Comme cette onde est caractérisée par le champ électrique et le champ magnétique on se doute que l'énergie véhiculée dépendra de ces deux quantités.
Si l'on considère l'onde plane harmonique se propageant dans le vide (exemple une radiation particulière du spectre du soleil), on sait que cette radiation transporte de l'énergie à travers le vide. C'est la base même de l'utilisation de l'énergie solaire ou plus prosaïquement de l'art de se faire bronzer au soleil sur la plage. Une onde de ce type présente une valeur moyenne nulle au cours du temps. Il est donc clair que l'énergie reçue par une surface donnée ne peut pas être proportionnelle à la valeur moyenne du champ électrique ou du champ magnétique. En effet lorsqu'une onde tombe sur un récepteur lumineux, le récepteur (oeil, film, ect..) ne perçoit pas l'amplitude du champ mais une quantité égale au carré du module du champ. L'argument est semblable en tous points à celui utilisé en électricité pour calculer l'énergie dissipée dans une résistance parcourue par un courant électrique.
Fondamental :
Nous appellerons donc l'intensité lumineuse
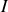de l'onde (où encore éclairement) le module au carré du champ électrique et nous retiendrons donc que pour une onde plane :
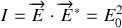
D'une façon beaucoup plus générale, l'intensité que peut mesurer un détecteur est la valeur moyenne de l'intensité de l'onde prise sur le temps de réponse du détecteur
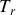soit
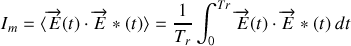
ce qui conduit pour l'onde plane monochromatique à
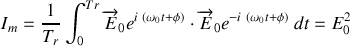
Remarque :
L'intensité lumineuse est nécessairement une quantité réelle comme le montre l'introduction du module du champ.
Si l'on travaille avec des champs réels la définition de l'intensité doit être corrigée d'un facteur 2 pour être compatible avec le calcul fait en complexe. De plus pour l'onde monochromatique périodique de période
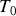le temps d'intégration est ramenée à la période
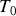car intégrer sur une période est équivalent à intégrer sur autant de périodes que l'on veut. On a alors
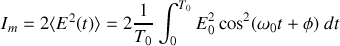
soit
Pour des champs non stationnaires c'est à dire des champs dont la valeur moyenne dépend de l'origine prise pour faire la mesure on définit l'intensité par
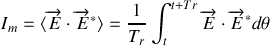
Remarque :
En optique l'onde a une pulsation très élevée de l'ordre de
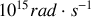soit une période très petite de l'ordre de
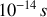. Les détecteurs usuels ne peuvent pas intégrer l'énergie instantanée à ce rythme. Leur temps de réponse est beaucoup plus grand. L'oeil a par exemple un temps de réponse de l'ordre du 1/10ème de seconde.
Les considérations physiques que nous avons utilisées pour présenter la notion d'intensité lumineuse peuvent être formalisées de façon beaucoup plus mathématique en utilisant le flux du vecteur de Poynting
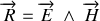
En tout point de l'espace l'onde électromagnétique émise par la source véhicule de l'énergie. La densité volumique d'énergie en un point quelconque ou existe le champ est donnée par
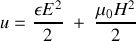
Si l'on tient compte de la valeur de
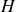, il vient
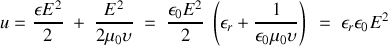
L'énergie qui est contenue dans un volume élémentaire s'appuyant sur une surface
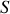est
et le flux instantané à travers cette surface est donc
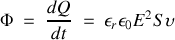
Il s'ensuit que l'éclairement de la surface est donné par
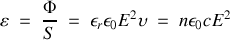
A une constante près l'éclairement est donc proportionnel au carré du champ
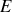et l'intensité mesurée par le détecteur est proportionnelle à la valeur moyenne de l'éclairement.
