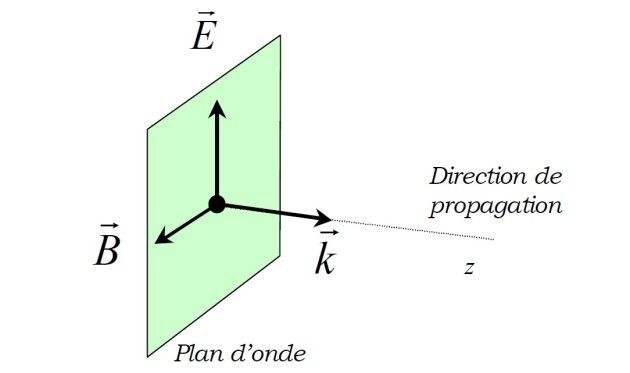
Présentation de l'onde harmonique plane
L'onde lumineuse est dite plane si le vecteur d'onde
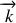 qui définit sa direction de propagation est constant en sens et en direction. Cette direction est appelée la direction de propagation de l'onde et le plan perpendiculaire au vecteur
qui définit sa direction de propagation est constant en sens et en direction. Cette direction est appelée la direction de propagation de l'onde et le plan perpendiculaire au vecteur
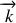 contenant les vecteurs
contenant les vecteurs
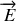 et
et
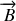 est appelé plan d'onde. L'onde est dite monochromatique si le vecteur d'onde est de module constant. Elle est dite harmonique si les variations spatiales et temporelles sont sinusoïdales.
est appelé plan d'onde. L'onde est dite monochromatique si le vecteur d'onde est de module constant. Elle est dite harmonique si les variations spatiales et temporelles sont sinusoïdales.
Expression du champ électrique
En un point
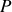 de l'espace et à l'instant
de l'espace et à l'instant
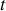 quelconque, l'onde lumineuse monochromatique peut être décrite par le champ électrique instantané
quelconque, l'onde lumineuse monochromatique peut être décrite par le champ électrique instantané
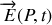 donné par :
donné par :
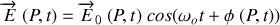
ou
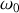 représente la pulsation de l'onde.
représente la pulsation de l'onde.
La valeur du champ électrique dépend donc :
de la position P du point considéré c'est la variable d'espace
du temps t ou l'on détermine le champ c'est la variable temporelle.
Le vecteur
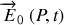 définit la direction de polarisation de l'onde. Il est existe de nombreux types de polarisation mais nous nous bornerons par la suite à étudier des ondes polarisées rectilignement pour lesquelles le vecteur
définit la direction de polarisation de l'onde. Il est existe de nombreux types de polarisation mais nous nous bornerons par la suite à étudier des ondes polarisées rectilignement pour lesquelles le vecteur
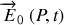 est constant.
est constant.
Remarque :
La phase
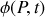 de l'onde au point
de l'onde au point
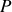 et à l'instant
et à l'instant
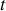 dépend de la position relative de la source
dépend de la position relative de la source
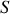 et du point
et du point
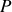 atteint par l'onde. Nous verrons plus tard que pour de nombreuses sources lumineuses, la phase à la source peut fluctuer au cours du temps. A la source
atteint par l'onde. Nous verrons plus tard que pour de nombreuses sources lumineuses, la phase à la source peut fluctuer au cours du temps. A la source
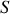 , on pourra donc écrire que le champ est défini à l'instant
, on pourra donc écrire que le champ est défini à l'instant
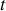 par :
par :
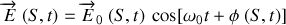
avec
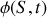 la phase à la source.
la phase à la source.
Onde progressive
Une onde est dite progressive si elle se propage dans l'espace au cours du temps. Pour une onde progressive il existe un lien entre l'onde observée en
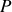 et l'onde émise par la source. L'onde qui arrive au temps
et l'onde émise par la source. L'onde qui arrive au temps
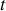 au point
au point
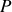 d'observation est la même que celle qui a été émise par la source un certain temps
d'observation est la même que celle qui a été émise par la source un certain temps
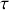 précédent le temps
précédent le temps
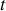 . Comme les ondes lumineuses se propagent à la vitesse de la lumière, le retard
. Comme les ondes lumineuses se propagent à la vitesse de la lumière, le retard
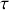 entre l'instant de l'émission de l'onde en
entre l'instant de l'émission de l'onde en
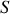 et celui de son observation en
et celui de son observation en
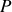 est
est
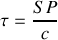
Il en résulte que le champ électrique au point
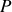 sera donné par :
sera donné par :
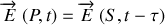
Soit
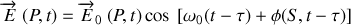
Le développement de l'argument du cosinus conduit à :
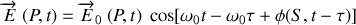
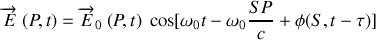
Il convient de faire apparaître le module du vecteur d'onde de propagation défini par
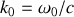 dans l'équation ci-dessus. On obtient alors
dans l'équation ci-dessus. On obtient alors
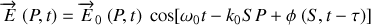
Il s'ensuit que pour
 la phase de l'onde au point
la phase de l'onde au point
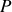 est donnée par
est donnée par
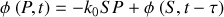
Attention :
La phase de l'onde au point
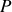 est donc la somme d'un terme de propagation,
est donc la somme d'un terme de propagation,
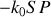 , et d'un terme lié à l'émission de l'onde par le point source
, et d'un terme lié à l'émission de l'onde par le point source
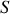 .
.
Remarque :
Si l'onde se propage dans un milieu d'indice de réfraction
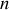 alors un raisonnement analogue au précédent tenant compte du changement de célérité de propagation
alors un raisonnement analogue au précédent tenant compte du changement de célérité de propagation
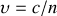 dans le milieu d'indice
dans le milieu d'indice
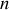 conduit à :
conduit à :
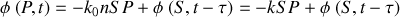
ce qui montre que le vecteur d'onde de propagation dans le milieu devient
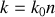
Onde plane polarisée rectilignement
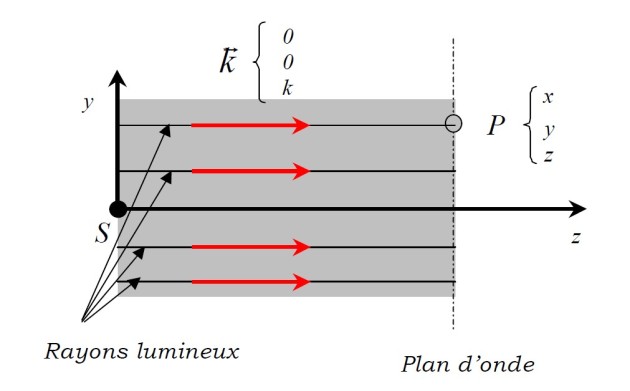
Une onde est dite plane, si le vecteur d'onde de propagation
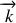 qui la décrit est constant. Il s'ensuit qu'une onde plane se propage dans une seule direction. Si elle est étendue (voir figure 2) elle est alors constituée d'une multitude de rayons lumineux tous parallèles les uns aux autres. Chaque rayon est issu d'un point source
qui la décrit est constant. Il s'ensuit qu'une onde plane se propage dans une seule direction. Si elle est étendue (voir figure 2) elle est alors constituée d'une multitude de rayons lumineux tous parallèles les uns aux autres. Chaque rayon est issu d'un point source
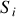 qui lui est propre. Si l'on admet que la propagation se fait dans la direction des
qui lui est propre. Si l'on admet que la propagation se fait dans la direction des
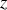 croissants et si l'on choisit comme origine de l'axe des
croissants et si l'on choisit comme origine de l'axe des
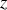 le point
le point
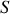 , la phase au point
, la phase au point
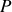 s'écrit :
s'écrit :
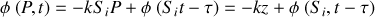
soit
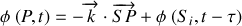
La différence de phase
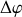 entre la phase de l'onde en
entre la phase de l'onde en
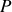 et celle de l'onde à la source est donc
et celle de l'onde à la source est donc
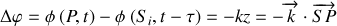
Pour des raisons de commodité, on convient souvent de prendre l'origine des phases à la source et on pose
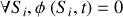
Dans ce cas l'onde plane s'écrit
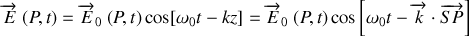
Il est intéressant de constater que la différence de phase
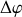 est constante si
est constante si
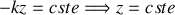
Le lieu des points équiphases est donc le plan
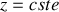 . Ce plan est un plan perpendiculaire au vecteur d'onde qui définit la direction et le sens du rayon lumineux. Ce résultat est conforme au théorème de Malus qui stipule que les rayons lumineux sont perpendiculaires aux surfaces d'onde. Il est facile de voir que tous les plans perpendiculaires à la direction
. Ce plan est un plan perpendiculaire au vecteur d'onde qui définit la direction et le sens du rayon lumineux. Ce résultat est conforme au théorème de Malus qui stipule que les rayons lumineux sont perpendiculaires aux surfaces d'onde. Il est facile de voir que tous les plans perpendiculaires à la direction
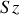 sont aussi des plans équiphases.
sont aussi des plans équiphases.
Remarque :
Quand le champ
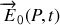 est constant au cours du temps et dans l'espace, l'onde est dite polarisée rectilignement. Le plan qui contient à la fois le vecteur d'onde
est constant au cours du temps et dans l'espace, l'onde est dite polarisée rectilignement. Le plan qui contient à la fois le vecteur d'onde
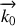 et le champ
et le champ
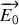 est appelé le plan de polarisation. Si la phase à l'origine est prise nulle à la source quel que soit l'instant considéré, une onde plane polarisée rectilignement s'écrit
est appelé le plan de polarisation. Si la phase à l'origine est prise nulle à la source quel que soit l'instant considéré, une onde plane polarisée rectilignement s'écrit
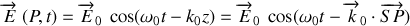
Nous verrons par la suite que cette situation correspond à une onde rigoureusement monochromatique appelée onde lumineuse idéalement cohérente à la fois dans le temps et dans l'espace car elle correspond à des trains d'onde d'extension infinie dans le temps et la phase de l'onde est identique pour tous les points contenus dans les plans perpendiculaires à sa direction de propagation.
Dans le vide (ou l'air) le module du vecteur d'onde de propagation est lié à la pulsation
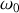 de l'onde par la relation :
de l'onde par la relation :
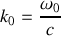
En explicitant la pulsation de l'onde, il est possible d'introduire la longueur d'onde qui est la distance parcourue par l'onde en une période temporelle
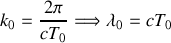
Attention :
En optique il est courant de présenter l'onde plane polarisée rectilignement sous la notation complexe suivante :
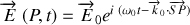
Cette notation est un abus d'écriture car nous aurions dû écrire que
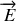 est la partie réelle de ce nombre complexe.
est la partie réelle de ce nombre complexe.