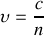Equations de Maxwell dans un milieu
Remarque :
Dans un milieu matériel quelconque, les équations de Maxwell valables dans le vide doivent être corrigées pour tenir compte de l'éventuelle anisotropie du milieu ainsi que de ses propriétés optiques.
En particulier au lieu de ne considérer que les champs
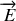et
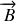, on décrit l'onde électromagnétique par quatre grandeurs vectorielles qui sont
,
,
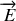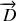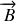et
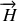, appelées respectivement champ et déplacement électrique et l'induction et l'excitation magnétique. Dans les milieux optiquement transparents l'induction est proportionnelle à l'excitation magnétique
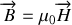
La situation est moins simple pour les grandeurs électriques car le déplacement dépend du champ électrique par le biais d'une relation tensorielle
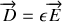
ou
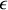est le tenseur de rang 2 de permittivité diélectrique du milieu. Ce tenseur se réduit à une constante si le milieu est isotrope. Dans ce cas le déplacement est proportionnel au champ.
Les équations de Maxwell dans un milieu matériel deviennent
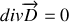
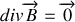
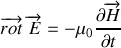
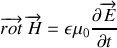
Solutions de l'équation de Maxwell
Nous considérons des solutions sous la forme d'ondes harmoniques planes du type
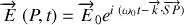
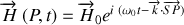
En reportant ces solutions dans les équations il est facile de voir que les champs doivent vérifier :
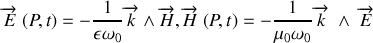
Pour l'onde T.E.M. valide dans les milieux isotropes, les champs ont pour expression
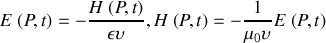
ou
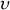est la célérité de propagation de la lumière dans le milieu matériel.
Relation de dispersion
Ces dernières relations conduisent par combinaison à l'équation de dispersion
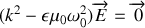
Il s'ensuit que le vecteur d'onde de propagation dans le milieu doit vérifier
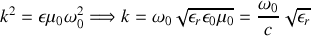
Le vecteur d'onde de propagation dans un milieu matériel diffère de celui dans le vide,
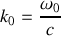, par la quantité
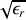. Cette quantité est par définition l'indice de réfraction du milieu
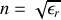
Il s'agit d'une relation de dispersion parce que la constante diélectrique relative
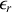dépend de la pulsation
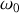de l'onde incidente. L'indice de réfraction dépend donc de cette pulsation.
Il résulte de cette présentation que dans un milieu matériel :
le vecteur d'onde est supérieur à celui du vide et la longueur d'onde inférieure à celle observée dans le vide
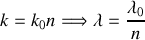
Dans un verre d'indice 1.5, la longueur d'onde de propagation est réduite de cette valeur. Pourtant un observateur ne peut pas percevoir ce changement car il reçoit sur sa rétine le rayon lumineux de longueur d'onde
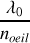quelle que soit la nature des milieux dans lesquels le rayon initial se sera propagé. Notre oeil est donc sensible à la longueur d'onde initiale.
la célérité de propagation de la lumière est inversement proportionelle à l'indice de réfraction
