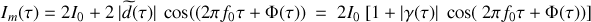On suppose que la lumière étudiée est quasi-monochromatique, de fréquence centrale
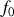et de largeur
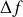. La densité spectrale s'écrit
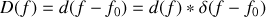
avec
une fonction décrivant la façon dont le spectre est centré sur
.
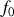Densité spectrale d'une source lumineuse. Dans cet exemple nous avons pris une densité spectrale gaussienne centrée sur
Nous supposons que l'onde issue de cette source lumineuse peut être divisée en amplitude ou en front d'ont d'onde de façon à faire interférer les signaux lumineux
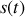et
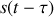qui résultent de cette division. On pourra considérer par exemple le montage des fentes d'Young :
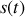et
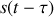sont les signaux arrivant au point
d'observation issus respectivement de la fente supérieure et inférieure.
La fonction de corrélation de l'amplitude complexe de ces deux signaux s'écrit alors
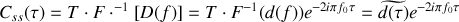
Posons
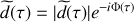
L'intensité moyenne produite par l'interférence de deux signaux lumineux
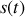et
se superposant avec un décalage
, s'écrit alors
Nous supposons que le signal lumineux
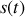est stationnaire ce qui impose
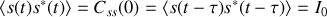
D'autre part nous avons
Il s'ensuit que
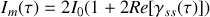
Soit
