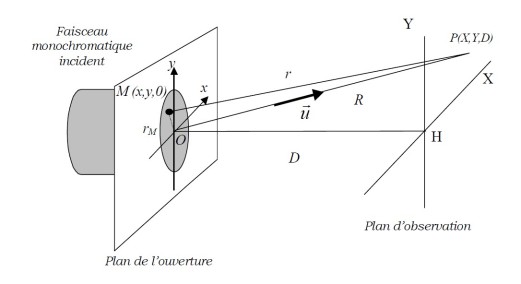
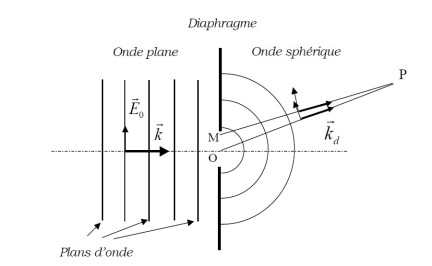
Nous considérons la diffraction d'une onde plane progressive (voir figure 7) arrivant sur un dia­phragme plan dont le centre est localisé en un point 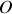. La direction de propagation de l'onde incidente est selon 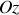et le diaphragme est dans le plan 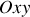.L'observation est faite sur un écran placé à une distance 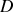de .

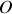L'onde incidente qui arrive sur le diaphragme est une onde plane polarisée recti­lignement. Tous les points du diaphragme sont donc en phase et vont se comporter comme des sources secondaires synchrones. En vertu du principe de Huygens-Fresnel, les sources secondaires vont émettre des ondes sphériques qui vont venir se superposer au point .

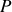En tout point 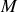du diaphragme, l'onde incidente plane est représentée en prenant arbitrairement l'origine des phases sur le diaphragme par

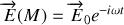
Après la traversée du diaphragme, cette onde devient sphérique et se propage donc dans tout le demi-espace en aval du diaphragme comme le montre la figure 8. Il n'y a plus une seule direction de propagation mais une infinité de directions. Le champ électrique dans chaque direction de propagation est transverse ce qui entraîne qu'à chaque direction de propagation il y ait une direction de polarisation de la lumière. Formulé de cette façon, nous voyons que le problème du calcul du champ en un point 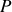de l'espace va être délicat à effectuer. C'est pour cette raison que nous allons proposer quelques approximations que nous allons maintenant justifier.

Figure 7 : Représentation schématique des conditions expérimentales de diffraction par un diaphragme plan

Figure 8 : Transformation d'une onde plane monochromatique en une onde sphérique au passage par un point O du diaphragme. Chaque point du diaphragme crée son propre système d'ondes sphériques. Toutes ces ondes interfèrent entre elles pour produire la figure de diffraction.