Dans un premier temps pour permettre le calcul de l'intégrale nous faisons l'hypothèse que la distance
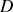est très supérieure aux distances
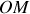et
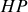. Comme la racine carré est approximée au premier ordre, nous pouvons qualifier cette approximation d'approximation parabolique. Il s'ensuit que la distance
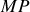s'écrit alors :
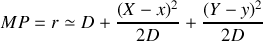
soit
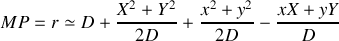
La fonction de transfert devient donc
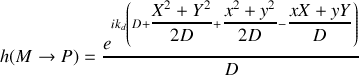
soit
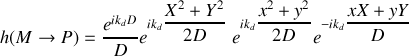
Le report de l'expression de
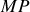dans l'équation donnant l'amplitude au point
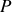conduit à :
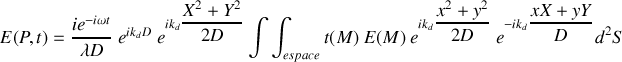
On voit bien que l'intégrale précédente appelée intégrale de Fresnel est difficile à calculer si le terme de phase
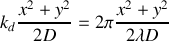n'est pas négligeable c'est à dire si la condition
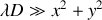n'est pas vérifiée. En considérant un point
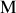de l'ouverture à 0.5mm de l'origine on voit que cette condition pour une longueur d'onde
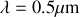conduit à
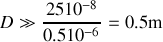
Attention :
Dans l'hypothèse où la condition de l'équation
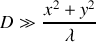n'est pas vérifiée on dit que l'on observe de la diffraction à distance finie ou diffraction de Fresnel. Si au contraire cette condition est vérifiée, il est possible de simplifier considérablement l'intégrale de Fresnel.
