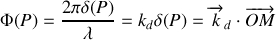L'approximation de Fraunhofer consiste à se placer à distance infinie du diaphragme. Dans ce cas, la première exponentielle sous l'intégrale tend vers 1 et l'expression de l'amplitude au point
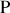devient beaucoup plus simple.
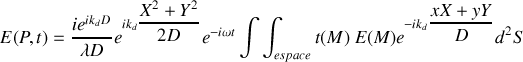
Remarque :
à l'issue de ce calcul le signe de la phase l'onde (le même que celui de l'exponentielle temporelle comme si l'onde considérée était régressive) ainsi que la phase additionnelle liée à
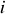. D'autre part si l'on considère l'équation aux dimensions nous voyons que
les exponentielles sont sans dimensions
l'intégrale est homogène à une surface
le produit
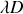homogène à une surface assure la cohérence des dimensions
L'expression ci-dessus est simplifiable si l'on tient compte du fait que l'écran est supposé fixe et que l'onde incidente est plane. En effet on a alors :
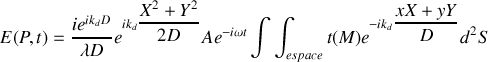
et le préfacteur qui se situe devant l'intégrale peut être considérer comme constant puisque les exponentielles complexes disparaîtront dans le calcul de l'intensité diffractée lorsqu'il sera multiplié par son conjugué. On obtient donc pour une distance
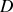et une longueur d'onde fixes l'expression suivante :
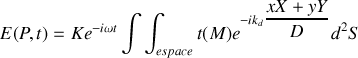
Le calcul de l'amplitude diffractée passe donc par l'évaluation de l'intégrale ci-dessus pour différents types de surface diffractante.
En introduisant les fréquences spatiales
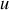et
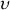définies par :
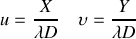
qui s'expriment en
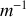et sont bien homogènes à des fréquences, il vient :
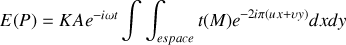
Cette expression peut se réécrire sous la forme :
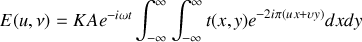
ce qui conduit au théorème suivant :
Théorème :
A distance infinie, l'amplitude diffractée par une pupille dans le plan d'observation est à une constante
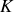près la transformée de Fourier bidimensionnelle de la transparence pupillaire
Remarque :
Si nous faisons apparaître le vecteur unitaire dans la direction moyenne d'observation pour un point d'observation
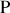peu éloigné du centre de l'écran
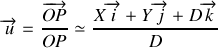
il est facile de voir que
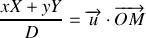
Cette quantité représente la différence de marche entre les ondes provenant du centre
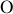de la pupille et celles issues d'un point
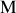quelconque dans l'ouverture.
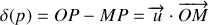
Il s'ensuit que l'argument de l'exponentielle peut s'écrire
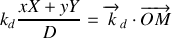
ce qui correspond à la différence de phase
:
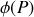