Le calcul du champ en
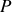 se simplifie grandement si l'on place l'écran à une distance suffisamment grande du diaphragme. Par suffisamment grand on entend que la distance
se simplifie grandement si l'on place l'écran à une distance suffisamment grande du diaphragme. Par suffisamment grand on entend que la distance
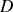 doit être très grande devant l'ouverture
doit être très grande devant l'ouverture
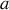 du diaphragme. Dans ce cas, les ondes sphériques issues du diaphragme vont arriver sur l'écran sous une incidence assez faible ce qui va nous permettre de considérer que toutes les ondes arrivant en
du diaphragme. Dans ce cas, les ondes sphériques issues du diaphragme vont arriver sur l'écran sous une incidence assez faible ce qui va nous permettre de considérer que toutes les ondes arrivant en
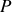 auront à peu près la même direction de propagation donc également à peu près la même polarisation (voir figure 8). Cette approximation consiste à dire que l'onde sphérique loin de la source est très proche d'une onde plane de vecteur d'onde
auront à peu près la même direction de propagation donc également à peu près la même polarisation (voir figure 8). Cette approximation consiste à dire que l'onde sphérique loin de la source est très proche d'une onde plane de vecteur d'onde
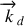 . Ce vecteur d'onde de diffusion
. Ce vecteur d'onde de diffusion
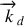 a sensiblement pour toutes les ondes qui arrivent en
a sensiblement pour toutes les ondes qui arrivent en
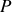 la même direction que le vecteur
la même direction que le vecteur
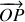 qui relie l'origine
qui relie l'origine
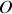 du diaphragme au point d'observation
du diaphragme au point d'observation
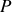 sur l'écran. Cela revient implicitement à considérer que les rayons lumineux sont peu inclinés sur l'axe, ce que l'on appelle l'approximation des rayons paraxiaux, et se propagent presque parallèlement entre eux.
sur l'écran. Cela revient implicitement à considérer que les rayons lumineux sont peu inclinés sur l'axe, ce que l'on appelle l'approximation des rayons paraxiaux, et se propagent presque parallèlement entre eux.
Les approximations suivantes
ondes scalaires
rayons paraxiaux
vecteur de diffusion
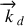 unique
unique
sont donc considérées comme valides pour calculer le champ créé en
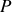 . L'intégrale de Fresnel-Kirchhoff devient donc
. L'intégrale de Fresnel-Kirchhoff devient donc
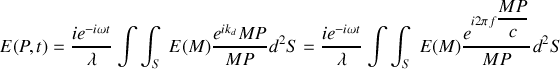
Remarque :
le facteur d'obliquité
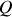 est égal à
est égal à
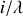 et il n'existe plus qu'un seul vecteur d'onde dans le terme de phase.
et il n'existe plus qu'un seul vecteur d'onde dans le terme de phase.
L'indroduction de la fonction de transfert conduit également à
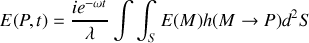
En utilisant la fonction de transparence du diaphragme (ou de la pupille) définie par :
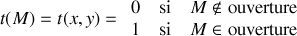
on peut étendre l'intégration à tout l'espace et généraliser le calcul sous la forme
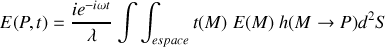
Pour calculer l'état vibratoire en
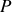 , il importe de calculer la distance
, il importe de calculer la distance
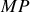 . Le point source
. Le point source
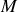 de coordonnées
de coordonnées
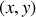 est distant de
est distant de
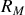 de
de
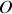 . Le point
. Le point
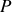 de l'écran de coordonnées
de l'écran de coordonnées
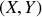 est distant de
est distant de
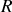 de
de
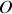 . Le vecteur
. Le vecteur
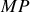 est donc donné par :
est donc donné par :
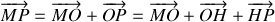
avec
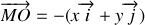
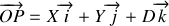
Il s'ensuit que
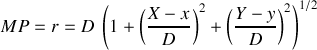
L'expression générale est donc obtenue en reportant la valeur de
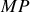 dans l'équation donnant l'amplitude diffractée. Il importe de remarquer que le calcul de l'intégrale dans ces conditions est difficile à faire voir impossible sans faire d'approximations sur la fonction de transfert
dans l'équation donnant l'amplitude diffractée. Il importe de remarquer que le calcul de l'intégrale dans ces conditions est difficile à faire voir impossible sans faire d'approximations sur la fonction de transfert
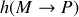 .
.




