Dans l'ensemble grand canonique, (potentiel chimique),volume et température sont fixés. Le nombre de particules est par contre variable : on peut voir cet ensemble comme une inclusion d'un tube à essai ouvert à l'intérieur d'un système fermé et thermostaté (ensemble canonique), lui-même inclus dans un univers à énergie conservée (ensemble micro-canonique).

Soit le volume du système thermostaté traité dans l'ensemble canonique, composé du système grand-canonique étudié, de volume supposé petit. Alors en notant le volume du reste du système on a :

De même pour le nombre de particules :

Soit la probabilité de trouver le système grand canonique dans l'état considéré. Cette probabilité est proportionnelle au nombre d'états accessibles au système, en étudiant l'ensemble microcanonique dans lequel il est inclus. Alors :

en inversant la formule de Boltzmann pour l'entropie de ce système microcanonique. Etudions à constant. Un développement autour de la valeur de référence du système canonique nous donne :

Calculons les deux dérivées partielles séparément.

Par le premier principe à constant et constant donc :

dans ces conditions.

A constant, constante et variable de même par définition du potentiel chimique :

donc :

Finalement :

On introduit la grande fonction de partition afin de calculer la constante de proportionnalité par normalisation des probabilités :

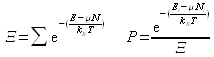
avec .

avec fonction de partition canonique, ou encore :

avec fugacité de la molécule.

Pour un gaz parfait .

Dans le chapitre sur l'entropie on a montré que :

Si nous calculons l'énergie libre de Gibbs par la relation :

nous obtenons donc :

or nous avons le résultat classique :

ou encore par le premier principe :

or :

Donc :

et encore une fois il est possible de calculer une grandeur supplémentaire (la pression) à partir de la fonction de partition.

Si on connaît on peut déduire l'enthalpie et l'enthalpie libre à partir des équations suivantes :

Si maintenant on définit le grand potentiel à partir de la grande fonction de partition par , calculons le nombre de particules moyen dans l'ensemble grand-canonique :

et on obtient donc facilement le nombre moyen de particules à partir du grand potentiel. Nous verrons que cette formule trouve son utilité dans l'étude de l'adsorption de molécules sur un catalyseur par exemple, comme dans l'étude des statistiques quantiques du chapitre suivant.