Le système appelé précédemment ensemble microcanonique (dont l'énergie est fixée à une petite variation près) ne nous permet pas facilement d'étudier les effets de la température sur les fonctions thermodynamiques. Cet ensemble correspond, en thermodynamique classique, à « l'univers »
. Dans la plupart des cas usuels, il vaut mieux considérer un système bien plus petit, inclus dans le précédent, dont l'énergie totale n'est pas fixée mais la température l'est à une fluctuation près : un système thermostaté, inclus dans un grand thermostat isolé, dont l'énergie totale est fixée, et la taille suffisamment grande pour absorber les fluctuations de température du système. Cet ensemble, en physique statistique, est dit ensemble canonique.
Le coup de génie de Gibbs a ainsi été de considérer un ensemble imaginaire de répliques d'un système en interaction (d'où le nom d' « ensemble »
) qui peuvent échanger entre eux par exemple de l'énergie (ici l'énergie de chaque réplique n'est pas fixée mais celle de l'ensemble des répliques l'est, formant ainsi un système de grande taille, cette fois ci considéré comme un système micro-canonique).
Soient des répliques constituées de ![]() particules et un ensemble de
particules et un ensemble de ![]() répliques formant un système micro-canonique, le poids d'une configuration est donc donné par la relation suivante :
répliques formant un système micro-canonique, le poids d'une configuration est donc donné par la relation suivante :
avec ![]() nombre de répliques qui ont une énergie
nombre de répliques qui ont une énergie ![]() , comme vu dans le chapitre sur l'ensemble microcanonique.
, comme vu dans le chapitre sur l'ensemble microcanonique.
La probabilité de trouver la réplique dans l'état ![]() est de même :
est de même :
avec ![]() l'énergie de la réplique
l'énergie de la réplique ![]() et
et ![]() fonction de partition canonique obtenue en sommant sur les répliques et non plus sur les états possibles d'une particule individuelle.
fonction de partition canonique obtenue en sommant sur les répliques et non plus sur les états possibles d'une particule individuelle.
On suppose l'équipartition de l'énergie entre les répliques. En notant ![]() alors l'énergie interne moyenne d'une réplique vaut :
alors l'énergie interne moyenne d'une réplique vaut :
résultat assez similaire à celui obtenu dans le chapitre précédent.
De la même façon admettons pour le moment ![]() , pour l'entropie d'une réplique nous avons
, pour l'entropie d'une réplique nous avons ![]() ou
ou ![]() .
.
Dans le chapitre précédent nous avions établi l'expression de l'entropie ; en reprenant pour ![]() systèmes on obtient :
systèmes on obtient :
soit ![]() en admettant de même que
en admettant de même que ![]() . On peut donc utiliser les formules pour énergie et entropie dans l'ensemble canonique en oubliant toute mention du nombre de répliques
. On peut donc utiliser les formules pour énergie et entropie dans l'ensemble canonique en oubliant toute mention du nombre de répliques![]() .
.
Pour N particules composant la réplique son énergie ![]() vaut, en sommant sur les niveaux :
vaut, en sommant sur les niveaux :
donc :
en sommant sur les ![]() répliques.
répliques.
Mais comme chaque particule visite tous les états (ergodicité) on peut permuter la somme sur les répliques et le produit sur les niveaux (pour s'en convaincre, prendre un exemple de 2 niveaux et 3 répliques par exemple, comme nous le ferons dans le chapitre sur les statistiques quantiques).
Dans le cadre de particules identiques mais obéissant à la mécanique classique nous verrons rigoureusement dans le chapitre sur les statistiques quantiques que :
Exemple :
Prenons le gaz parfait à ![]() particules.
particules.
![]() fonction de partition d'une particule,
fonction de partition d'une particule,
![]() fonction de partition pour
fonction de partition pour ![]() particules indiscernables,
particules indiscernables,
l'entropie vaut donc :
avec la formule de Stirling.
si on pose ![]() ,
, 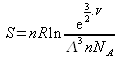 .
.
Pour un gaz parfait ![]() donc
donc 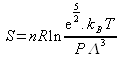 constituant la formule de Sackur-Tetrode qui donne l'entropie absolue d'un gaz parfait.
constituant la formule de Sackur-Tetrode qui donne l'entropie absolue d'un gaz parfait.
Si on passe d'un volume ![]() à un volume
à un volume ![]() à T constante, on a :
à T constante, on a :
On peut également résoudre ce problème à l'aide du premier principe de la thermodynamique.
![]() car
car ![]() est constante, donc
est constante, donc ![]() et
et ![]() . Soit :
. Soit :
or ![]() ,
,
donc ![]() et
et ![]() .
.
On obtient également :
ce qui nous rassure sur la cohérence de la physique statistique et de la thermodynamique classique. Remarquons que sans le terme en ![]() dans la fonction de partition des particules indiscernables nous n'aurions pas eu ce résultat.
dans la fonction de partition des particules indiscernables nous n'aurions pas eu ce résultat.



