L'entropie, d'abord définie par Carnot et Clausius dans la première partie du XIXème siècle, est une quantité qui permet de prévoir le sens d'une réaction spontanée, par exemple le sens du transfert de chaleur entre deux objets à température différente mis en contact.

Soit cette fonction d'état ; dans un transfert thermique cette grandeur varie de (voir le cours de thermodynamique).

Par exemple, lorsque deux corps à température différente sont mis en contact, ces températures s'égalisent et l'entropie totale augmente bien que le bilan des chaleurs échangées soit nul ; au passage, le désordre a augmenté.

La théorie de Boltzmann permet de faire le lien entre l'entropie et le désordre.

A l'équilibre on définit avec nombre d'états accessibles au système ou encore avec poids de la configuration la plus probable vue au chapitre précédent. On définit encore :

avec probabilité de trouver le système dans l'état i.

Ici représente la néguentropie (ou entropie avec le signe - ) d'information, qui permet d'évaluer la quantité de désordre du système. Cette quantité est par exemple employée en traitement du signal, ou dans les logiciels de compression de données pour en évaluer l'efficacité.

• Si le système est ordonné on a par exemple un premier état :

• Si le système est parfaitement désordonné toutes les probabilités sont égales et 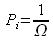, alors 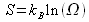et on retrouve la définition de Boltzmann.

Essayons de relier ces définitions entre elles : définition de thermodynamique classique, et définition de Boltzmann, par les résultats des chapitres précédents.

On avait trouvé pour l'énergie interne :

avec l'énergie « de point zéro » constante.

et donc :

Le premier terme permet de changer les valeurs des niveaux à populations constantes (typiquement en changeant la taille de la boîte de confinement pour un gaz parfait, par exemple revoir le résultat obtenu ci dessus ), donc d'apporter de l'énergie sans modifier le désordre.

Par identification avec le premier principe cette quantité correspond à du travail ordonné en présence de forces de pression uniquement

Le deuxième terme permet de changer les populations à niveaux constants (changement d'énergie sans travail, donc uniquement thermique) correspondant à la quantité classique dans le cas réversible.

Finalement :

on pose donc :

A partir de la définition de Boltzmann, par ailleurs :

Rappelons nous que 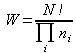comme démontré dans le chapitre précédent.

donc :

d'après la formule de Stirling pour le logarithme :

On a alors :

donc puisque  :

et comme comme établi précédemment, donc :

avec et .

On a bien :

Si nous reprenons la définition de l'entropie d'information :

comme ,

or :

on retrouve encore une fois le résultat donc les définitions sont cohérentes.

D'autre part nous avons démontré que :

donc :

avec et .

Soit :

ou encore :

avec .

Remarquons que les quantités thermodynamiques et peuvent être calculées à partir de la fonction de partition ; nous verrons que les autres quantités usuelles (pression, énergie libre...) pourront aussi être calculées à partir de cette même fonction.