Nous allons commencer par considérer une situation microscopique isolée, traitée d'abord en mécanique quantique, mais en supposant que les atomes ou molécules constituant le système sont certes identiques, mais « discernables »
(Boltzmannions) dans le sens où on peut les suivre au cours du temps et les identifier individuellement (pas de recouvrement des fonctions d'onde quantiques).
On considère donc 
atomes, molécules ou particules dont l'énergie totale 
est fixée à 
près.
Ces
molécules identiques mais discernables sont distribuées par paquets de 
sur des niveaux quantifiés d'énergie 
avec par convention 
. Par conséquent :
On suppose que les
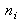sont à l'équilibre (ne changent pas au cours du temps) ou proches de l'équilibre (petites fluctuations).On suppose que toutes les distributions donnant une même énergie
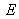sont équiprobables.
On définit le poids 
d'une distribution des molécules sur les niveaux :
Le lecteur est encouragé à prendre l'exemple de quelques petits systèmes (2 atomes sur 3 niveaux, 3 atomes sur 2 niveaux, etc) pour se convaincre de la validité de cette formule dans le cas de particules identiques mais discernables.
Cherchons la configuration dominante, ce qui correspond au maximum de 
et donc au maximum de 
. Comme :
d'après la formule de Stirling pour le logarithme :
On a alors : 
puisque 
.
L'extrémum serait a priori donné par :
On ne peut pas écrire directement que chacune des dérivées partielles est nulle car les 
ne sont pas indépendants (la somme des 
est fixée à N, et de plus 
). On utilise donc la théorie des multiplicateurs de Lagrange, qui permet, en différenciant chacune de ces deux contraintes, en les multipliant par les facteurs 
et 
d'obtenir des variations indépendantes des 
en les rajoutant à l'équation de départ, soit :
alors :
alors :
donc :
et comme 
on a donc 
soit 
ce qui fixe le premier multiplicateur de Lagrange :
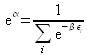
Donc la probabilité 
de trouver le système sur le niveau i est :
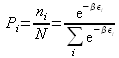
C'est l'état le plus probable du système à l'équilibre. On reconnaît une distribution de Boltzmann déjà vue en théorie cinétique des gaz (distribution de Maxwell-Boltzmann des vitesses).
On définit la fonction de partition 
(parfois notée 
) par :
avec la probabilité 
.
Nous verrons plus tard en comparant certains résultats avec ceux de la thermodynamique classique que 
avec : 
constante de Boltzmann égale au rapport de la constante des gaz parfaits et du nombre d'Avogadro, et
la température absolue (en Kelvin).
Exemple : 1
Soit un système à deux niveaux d'énergie 
et 
, calculer la probabilité 
et 
de trouver le système dans chacun des deux niveaux.
Solution :
La fonction de partition de ce système est :
alors la probabilité vaut :
et 
.
La somme des probabilités est bien égale à 1.
Exemple : 2
Chercher la fonction de partition d'un oscillateur harmonique quantique en fixant le premier niveau à 0 (en principe 
, mais on prendra 
).
Solution :
La fonction de partition d'un oscillateur harmonique est :
On peut remarquer que c'est une suite géométrique de raison 
et de premier terme égal à 1
d'où :
(fonction de partition d 'un oscillateur harmonique).
Exemple : 3
Calculer l'énergie moyenne 
d 'un oscillateur harmonique quantique.
Solution :
(espérance de l'énergie)
or 
et 
alors 
On remarque que :
d'où : 
On a la fonction de partition d'un oscillateur harmonique : 
déterminée précédemment
Donc, pour N oscillateurs harmoniques :
donc l'énergie moyenne d'un système de N oscillateurs harmoniques vaut :
On peut remarquer qu'à basse température ( grand 
) cette énergie moyenne se concentre sur le premier niveau.
