On néglige les interactions entre les particules, alors l'énergie totale est purement cinétique. Pour une particule confinée dans une boîte de taille 
par un potentiel infini le Hamiltonien vaut :
avec P sa quantité de mouvement.
A une dimension
Posons l'équation de Schrödinger stationnaire :
avec 
et 
.
Les conditions aux limites fixes sont :
La solution de l'équation (1) s'écrit sous la forme :
La première condition aux limites
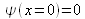donne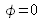 
La deuxième condition aux limites
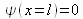donne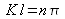 
Condition de normalisation :
alors : 
car 
.
On a donc en réinjectant dans l'équation de Schrödinger :
et nous remarquons que l'énergie est quantifiée.
A trois dimensions
Le hamiltonien 
s'écrit sous la forme :
La fonction d 'onde 
peut être séparée suivant les trois directions de l'espace car l'équation est linéaire.
L'énergie du système s' écrit :
L'équation 
donne que l'énergie du gaz parfait unidimensionnel peut se mettre, en décalant l'indice d'un cran pour partir de 0, sous la forme :
avec :
.
La fonction de partition du gaz parfait vaut donc :
En supposant que l'énergie 
varie d' une façon continue (ce qui est acceptable pour les grandes énergies) alors :
or 
donc par symétrie (fonction paire) : 
D'autre part, on a :
avec 
.
est dite longueur d'onde thermique de de Broglie. Remarquons que cette longueur est caractéristique du côté quantique du système : pour un système de grandes dimensions par rapport à elle, le système est classique. Ceci se produit pour des petites valeurs de 
, des grandes masses ou des températures élevées.
Généralisation à 3 dimensions :
La fonction de partition vaut 
à partir de la forme de l'équation de Schrödinger. Remarquons par exemple pour l'argon dans les conditions normales de température et de pression que cette longueur d'onde de de Broglie est très faible devant les distances moyennes interatomiques, donc les atomes d'argon dans ces conditions peuvent être traités par la mécanique classique. Par contre, pour l'hélium, plus léger, aux basses températures, ou pour des électrons d'un solide à température ambiante, confinées dans une maille cristalline, la longueur d'onde de de Broglie est plus grande que les dimensions caractéristiques du problème, ce qui implique un traitement purement quantique.
Calcul de l'énergie moyenne d 'un gaz parfait
En utilisant les formules vues précédemment :
or :
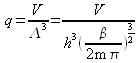
alors : 
.
En dérivant seul subsiste le terme en 
donc : 
, avec N le nombre de particules.
Pour n moles, le nombre de particules est 
avec 
.
la capacité calorifique vaut donc
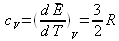pour le gaz monoatomique ce qui correspond à un résultat connu en thermodynamique classique. C'est un premier argument pour identifier le paramètre 
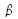avec la température thermodynamique 
,
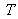pour le gaz diatomique nous verrons à la fin du cours que :
