Dans un volume égal à l'unité le nombre d'atomes de gaz parfait supposés obéir à la mécanique classique et ayant une vitesse comprise entre et est proportionnel au facteur de Boltzmann suivant , avec :

et donc :

ou , si on préfère exprimer en fonction des impulsions, la constante de normalisation étant différente (distribution de Maxwell-Boltzmann, établie au départ par Maxwell avec des arguments différents).

Soit N le nombre d'atomes présents dans le volume considéré ,

et on trouve que :

en employant (formule à retenir) :

Considérons désormais une paroi orthogonale à l'axe Ox et comptons le nombre de chocs atomiques sur cette paroi, comme la quantité de mouvement transférée par chaque choc : par la règle du parallélogramme. Comme la relation de Newton s'exprime sous la forme :

avec , ou .

La pression P qui s'exerce sur la paroi est la force moyenne par unité de surface. Seules les particules allant vers les x positifs vont frapper la paroi, à qui elles vont donc transférer par unité de temps la quantité de mouvement et donc la force .

Par ailleurs, le nombre de chocs est proportionnel à la surface considérée, plus précisément au nombre de particules présent dans un petit volume de surface et de longueur .

Finalement :

soit :

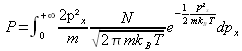
or on sait que :

et en dérivant par rapport à :

donc :

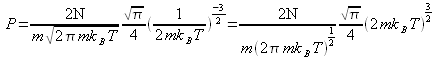
ce qui conduit à : pour un volume arbitraire et on retrouve bien la relation des gaz parfaits, ce qui est un deuxième argument pour justifier la valeur de .