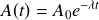Imaginons l'expérience suivante :
On place une source radioactive ponctuelle devant un compteur Geiger-Müller. On peut mesurer grâce à ce dispositif le nombre de désintégrations par seconde, c'est-à-dire l'activité de la source. On fait des mesures pendant un temps suffisamment long pour voir apparaître l'évolution dans le temps de cette activité.
On reporte les résultats sur un graphe : activité en fonction du temps.
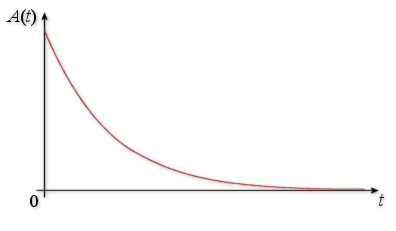
On obtient l'équation d'une courbe exponentielle. On montrera qu'elle est de la forme :
|
|---|
On constate qu'au bout d'un certain temps T, égal à la demi-vie (ou période) du nucléide radioactif, l'activité initiale est divisée par 2.
Au bout d'un temps égal à 2T, l'activité initiale est divisée par 4.
Au bout d'un temps égal à 3T, l'activité initiale est divisée par 8.
Etc.
Au bout d'un temps égal à nT, l'activité initiale est divisée par
.
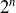InformationsRemarque :
En pratique, on peut considérer qu'au bout de 10 T environ l'activité est devenue négligeable par rapport à l'activité initiale (l'activité initiale étant alors divisée par
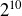soit environ 1 000).
