Par définition la demi-vie ou période radioactive T est le temps au bout duquel l'activité initiale de l'échantillon est divisée par deux. Pour obtenir T, il faut donc résoudre l'équation :
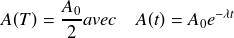
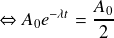
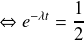
Rappel : Propriétés du logarithme népérien :
Le logarithme népérien est la fonction réciproque de l'exponentielle, autrement dit :
.
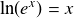De plus on a la relation :
.
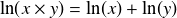D'où découlent les relations :
,
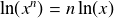et en particulier :
.
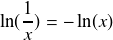On applique la fonction logarithme népérien de part et d'autre de l'équation :
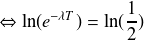
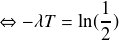
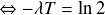
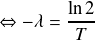
On obtient donc la relation :
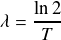
Attention :
Dans cette relation, on n'obtiendra
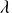en
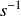(unité du Système International) que si la demi-vie T est exprimée en secondes.
