Les filtres réalisés à partir de dipôles passifs introduisent une atténuation du signal. L'emploi des amplificateurs opérationnels permet de réaliser simplement des filtres RC actifs dont les caractéristiques sont équivalentes à celles des filtres LC passifs. Il existe un nombre considérable de filtres actifs différents classés selon la forme de leur fonction de transfert en filtres de Butterworth, de Tchebychev, de Bessel ... Des ouvrages entiers sont consacrés à leur étude. Nous examinerons seulement quelques exemples simples.
Exemple de filtre du premier ordre
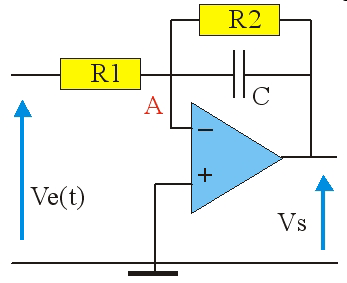
Soient Z_C l'impédance complexe du condensateur et Z_2 l'impédance qui relie le point A et la sortie : Z_2 =R_2Z_C/(R_2 + Z_C) = R_2/(1 + jR_2C\omega)
La fonction de transfert est donc (voir chapitre « Multiplicateur ») : H = – R_2/R_1(1 + jR_2C\omega)
On pose H_0 = –R_2/R_1 et \omega_c= 1/R_2\cdotC.
H = H_0/(1 + j\omega/ \omegac) = H_0/(1 + jx)
Ce circuit constitue un filtre passe-bas dont le gain est :
G=\vertH\vert=\frac{H_0}{\sqrt{1+(\omega /\omega_C)^2}
Sa fréquence de coupure (H = H_0/\sqrt2 est \omega_C. Si la résistance R_2 est trop grande, le montage se comporte alors en intégrateur (voir chapitre « Intégrateur idéal »).
Exemple de filtre du second ordre (Sallen et Key)
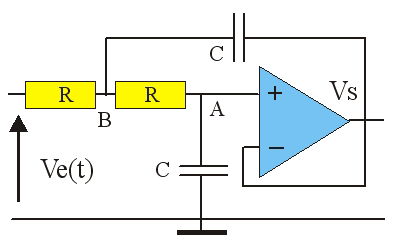
L'amplificateur est monté en suiveur : V_A = V_S
L'application du théorème de Millman en A et B donne :
\frac{V_B}{R}=V_S \left(\frac{1}{R}+\frac{1}{Z_C}\right)
V_B\left(\frac{2}{R}+\frac{1}{Z_C}\right)=\frac{V_E}{R}+\frac{V_S}{R}+\frac{V_S}{Z_C}
On en déduit : \frac{V_S}{V_E}=\frac{1}{1+\frac{2R}{Z_C}+\frac{R^2}{Z^2_c. En posant \omega0 = 1/RC et x = \omega/\omega_0, on tire :
H(j\omega)=\frac{1}{(1+jx)^2 soit : \vertH\vert=\frac{1}{1+x^2
C'est donc un filtre passe-bas du second ordre dont les deux pôles sont identiques. En permutant les deux résistances et les deux condensateurs on obtient un passe-haut. En permutant un condensateur et une résistance on obtient un passe-bande. Pour obtenir des filtres d'ordre plus élevés, on met plusieurs cellules (dont les fréquences de coupure sont différentes) en cascade.
Cliquez ici pour visualiser le fonctionnement du circuit.
On peut donner un gain à ce filtre en modifiant la rétroaction.
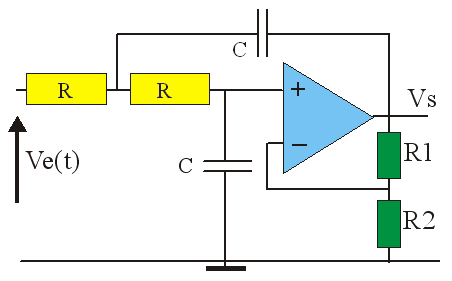
On pose k = (R_1 + R_2)/R_2. Un calcul analogue au précédent donne, pour la fonction de transfert, l'expression :
H(j\omega)=\frac{k}{1-x^2+j\cdotx(3-k)
Selon la valeur de k le comportement du filtre est modifié.
-
Si k = 1,586, on a la même réponse (plate avant la coupure) que pour le circuit précédent. (type Butterworth)
-
Si k < 1,586, le déphasage varie linéairement avec \omega. (type Bessel)
-
Si k > 1,586, la coupure est plus marquée mais il y a des oscillations avant celle-ci. (type Tchebychev)