L'énergie cinétique d'un solide
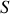dans un référentiel
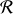est définie par
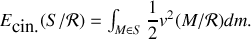
Le théorème de KOENIG de l'énergie cinétique permet de séparer deux contributions à cette énergie, une de translation de
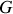dans le référentiel
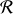et une autre de rotation dans le référentiel barycentrique :
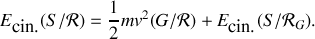
Dans le cas particulier de la rotation par rapport à un axe
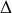fixe dans le référentiel
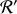considéré (qui peut être
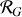) on obtient
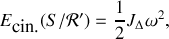
avec
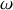vitesse angulaire de rotation autour de
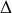, et
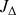moment d'inertie par rapport à
.
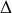Exemple :
énergie cinétique d'un cerceau circulaire de rayon
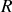, qui roule sans glisser sur un plan. Le théorème de Koenig permet d'écrire
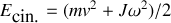, où
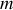est la masse de la roue et
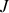son moment d'inertie par rapport à son axe. Tous les points de la roue étant situés à la distance
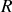de l'axe, l'intégrale définissant
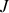se calcule directement :
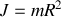. La traduction de l'absence de glissement entre la roue et le sol permet quant à elle d'écrire
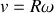d'où l'énergie cinétique totale de la roue :
.
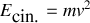