Soit
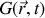 une grandeur attachée à une particule fluide (par exemple sa masse volumique, sa vitesse, la concentration locale d'un colorant...). Entre
une grandeur attachée à une particule fluide (par exemple sa masse volumique, sa vitesse, la concentration locale d'un colorant...). Entre
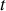 et
et
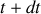 , la variation de
, la variation de
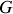 pour une même particule est :
pour une même particule est :
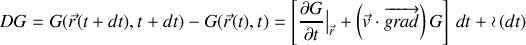
au premier ordre en
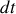 . On note
. On note
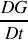 la dérivée particulaire ou dérivée en suivant le mouvement
la dérivée particulaire ou dérivée en suivant le mouvement
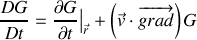
Le premier terme du membre de droite désigne la dérivée “usuelle” par rapport au temps, à position fixée, d'une fonction
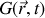 . L'opérateur (
. L'opérateur (
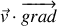 ) s'applique aussi bien à des grandeurs scalaires que vectorielles. En coordonnées cartésiennes :
) s'applique aussi bien à des grandeurs scalaires que vectorielles. En coordonnées cartésiennes :
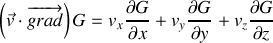
Dans le cas particulier où
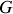 désigne la vitesse d'une particule fluide, on peut montrer que
désigne la vitesse d'une particule fluide, on peut montrer que
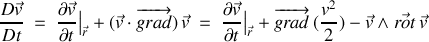
Attention :
L'équivalence de ces deux expressions de l'accélération d'une particule fluide est utile pour traiter certains problèmes de dynamique (relation fondamentale, bilan des forces...).




