Soit 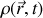la masse volumique du fluide. La conservation de la masse se traduit localement par l'équation dite de continuité :

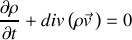
qui peut se réécrire

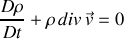
La particule fluide de masse volumique 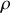 renferme une quantité de masse 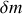dans un volume 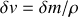. Si 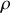 varie au cours du mouvement, c'est que le volume 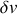varie ( 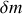est par construction constant, même si la particule fluide n'est pas toujours constituée des mêmes molécules, cf. partie A).

Ainsi,

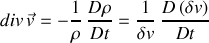
La divergence du vecteur vitesse 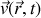est donc le taux d'accroissement du volume de la particule fluide située en 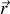à l'instant 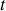. Si cette divergence est positive, le volume en question croît, si elle est négative, le volume se contracte.