Question 1
Un transfert thermique quasi-statique peut s'écrire en raison des capacités thermiques absolues
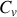 ou
ou
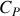 du système considéré et des coefficients thermométriques
du système considéré et des coefficients thermométriques
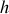 et
et
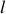 :
:
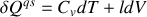 , en fonction des variables
, en fonction des variables
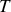 et
et
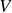 , où
, où
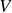 est le volume absolu.
est le volume absolu.
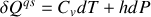 , en fonction des variables
, en fonction des variables
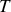 et
et
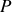 .
.
De plus, un travail mécanique quasi-statique est donné par
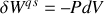 et le travail technique correspondant par
et le travail technique correspondant par
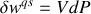 .
.
Déduire du premier principe l'écriture des différentielles
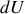 de l'énergie interne et
de l'énergie interne et
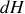 de l'enthalpie (
de l'enthalpie (
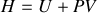 )
)
Question 2
Rappeler l'équation d'état d'un gaz parfait.
Donner la définition thermodynamique d'un gaz parfait (c'est-à-dire les deux lois de Joule relatives à l'énergie interne
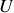 et à l'enthalpie
et à l'enthalpie
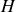 ).
).
Question 3
En fonction de la réponse à la question précédente, à quoi les coefficients thermométriques
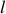 et
et
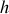 sont-ils égaux dans le cas du gaz parfait ?
sont-ils égaux dans le cas du gaz parfait ?
Expliquer aussi pourquoi les capacités thermiques molaires
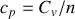 et
et
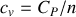 de
de
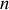 moles de gaz parfait ne peuvent éventuellement dépendre que d'un seul paramètre d'état, la température.
moles de gaz parfait ne peuvent éventuellement dépendre que d'un seul paramètre d'état, la température.
Question 4
Déduire de la question précédente les expressions différentielles
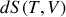 et
et
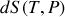 de l'entropie de
de l'entropie de
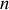 moles de gaz parfait (ces deux formes sont équivalentes).
moles de gaz parfait (ces deux formes sont équivalentes).
On prendra soin d'utiliser l'équation d'état des gaz parfaits afin d'éliminer
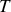 des rapports
des rapports
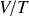 et
et
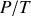 .
.
Question 5
En première approximation aux températures ordinaires, les capacités thermiques molaires
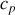 et
et
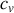 sont des constantes.
sont des constantes.
En utilisant les résultats de la question 3 et en se plaçant dans cette approximation, donner les valeurs des variations intégrales
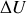 et
et
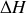 d'un gaz parfait entre deux états initial (i) et final (f).
d'un gaz parfait entre deux états initial (i) et final (f).
Donner enfin, en utilisant les réponses à la question 4, la variation
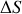 en fonction des variables
en fonction des variables
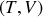 d'une part,
d'une part,
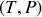 d'autre part.
d'autre part.
Question 6
À partir de la relation de Mayer pour un gaz parfait et de la définition du coefficient de Laplace
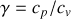 , exprimer les capacités thermiques molaires d'un gaz parfait en fonction de la constante
, exprimer les capacités thermiques molaires d'un gaz parfait en fonction de la constante
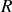 des gaz parfaits et de ce coefficient de Laplace.
des gaz parfaits et de ce coefficient de Laplace.



